
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
分析 (1)由频率分布直方图先求出成绩不小于130分为优秀,则成绩为优秀的频率,用分层抽样的方法从这500人中抽取5人的成绩进行分析,能求出成绩为优秀的学生人数.
(2)抽取的5名学生中,成绩为优秀的学生人数为2人,要随机抽取2名学生参加分析座谈会,基本事件总数n=${C}_{5}^{2}$=10,恰有1人成绩为优秀包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,同由此能过河卒子 同恰有1人成绩为优秀的概率.
解答 解:(1)由频率分布直方图知:
成绩不小于130分为优秀,则成绩为优秀的频率为:(0.06+0.02)×5=0.4,
∴用分层抽样的方法从这500人中抽取5人的成绩进行分析,
其中成绩为优秀的学生人数为:5×0.4=2人.
(2)在(1)中抽取的5名学生中,成绩为优秀的学生人数为2人,
要随机抽取2名学生参加分析座谈会,
基本事件总数n=${C}_{5}^{2}$=10,
恰有1人成绩为优秀包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,
∴恰有1人成绩为优秀的概率p=$\frac{m}{n}=\frac{6}{10}=0.6$.
点评 本题考查频率分布直方图、分层抽样的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
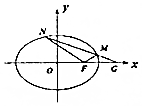 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其短轴为2,离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
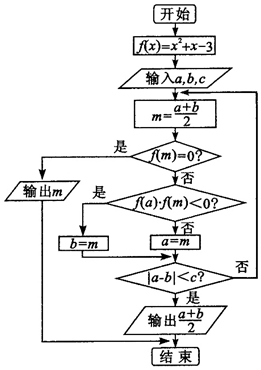
| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 169石 | B. | 192石 | C. | 1367石 | D. | 1164石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
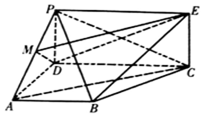 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 纤维长度 | 频数 |
| [22.5,25.5) | 3 |
| [25.5,28.5) | 8 |
| [28.5,31.5) | 9 |
| [31.5,34.5) | 11 |
| [34.5,37.5) | 10 |
| [37.5,40.5) | 5 |
| [40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
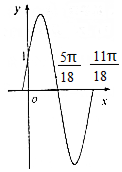 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com