
若x+yi=1+2xi(x,y∈R),则x﹣y等于( )
A.0 B.﹣1 C.1 D.2
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
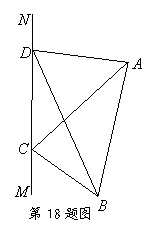 如图,为对某失事客轮
如图,为对某失事客轮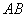 进行有效援助,现分别在河岸
进行有效援助,现分别在河岸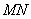 选择两处
选择两处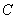 、
、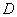 用强光柱进行辅助照明,其中
用强光柱进行辅助照明,其中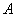 、
、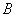 、
、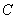 、
、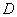 在同一平面内.现测得
在同一平面内.现测得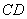 长为
长为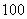 米,
米,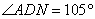 ,
,
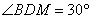 ,
,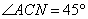 ,
,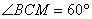 .
.
(1)求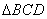 的面积;
的面积;
(2)求船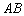 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
设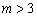 ,对于数列
,对于数列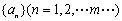 ,令
,令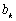 为
为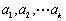 中的最大值,称数列
中的最大值,称数列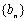 为
为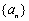 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列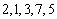 的递进上限数列为2,2,3,7,7.则下面命题中( )
的递进上限数列为2,2,3,7,7.则下面命题中( )
①若数列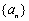 满足
满足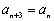 ,则数列
,则数列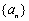 的递进上限数列必是常数列
的递进上限数列必是常数列
②等差数列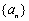 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列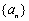 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
A. 0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com