
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,1) |
分析 由f(2-x)=f(x)得出函数的周期,由y=f(x)-loga(x+1)=0得到f(x)=loga(x+1),利用函数的周期性和偶函数的性质,分别作出函数y=f(x)和y=loga(x+1)的图象,利用图象确定a的取值范围.
解答 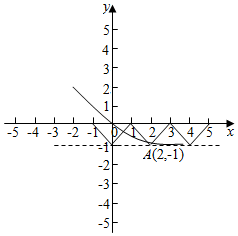 解:对任意x∈R都有f(2-x)=f(x)
解:对任意x∈R都有f(2-x)=f(x)
∴f(x)的周期是2,
且当x∈[0,1]时,f(x)=x-1,
∴x∈[-1,0]时,f(x)=-x-1,
若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,
即f(x)和y=loga(x+1)在(0,+∞)上至少有三个零点,
画出函数图象,如图示:
由图象得:${log}_{a}^{3}$>-1,解得;0<a<$\frac{1}{3}$,
故选:C.
点评 本题主要考查函数零点应用,利用数形结合,将方程转化为两个函数图象的相交问题是解决此类问题的基本方法.综合性较强.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)>0 | D. | f(x1)>0,f(x2)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 人体的脂肪含量与年龄之间没有相关关系 | |
| B. | 汽车的重量和汽车每消耗1L汽油所行驶的平均路程负相关 | |
| C. | 吸烟量与健康水平正相关 | |
| D. | 气温与热饮销售好不好正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
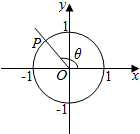
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com