
 易知n2=1+2+3+…+n+(n-1)+…+2+1,故有13=1,23=2•22=2(1+2+1)=2+4+2;33=3•32=3(1+2+3+2+1)=3+6+9+6+3,…,这些通过分拆得到的数可组成数阵认真观察数阵,可以求出和式S=13+23+33+…+203的值为
易知n2=1+2+3+…+n+(n-1)+…+2+1,故有13=1,23=2•22=2(1+2+1)=2+4+2;33=3•32=3(1+2+3+2+1)=3+6+9+6+3,…,这些通过分拆得到的数可组成数阵认真观察数阵,可以求出和式S=13+23+33+…+203的值为科目:高中数学 来源: 题型:
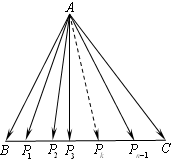 若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量
若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
| A、2 | B、1 | C、0 | D、-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、频率就是概率 |
| B、频率是客观存在的,与试验次数无关 |
| C、概率是随机的,在实验前不能确定 |
| D、随着试验次数的增加,频率一般会越来越接近概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、如果α⊥γ,β⊥γ,则α∥β | ||
| B、如果α⊥β,m∥α,则m⊥β | ||
C、如果m∥n,n
| ||
| D、如果m⊥α,n⊥α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com