练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    给出下列六个命题：
    ①两个向量相等，则它们的起点相同，终点相同；      
    ②若|
    a
    |=|
    b
    |，则
    a
    =
    b
    ；
    ③若
    AB
    =
    DC
    ，则四边形ABCD是平行四边形；
    ④平行四边形ABCD中，一定有
    AB
    =
    DC
    ；
    ⑤若
    m
    =
    n
    ，
    n
    =
    k
    ，则
    m
    =
    k
    ；
    ⑥
    a
    ∥
    b
    ，
    b
    ∥
    c
    ，则
    a
    ∥
    c
    ．
    其中不正确的命题的个数为（　　）
    A、2个B、3个C、4个D、5个
    考点：平面向量数量积的运算
    专题：平面向量及应用
    分析：①利用向量相等即可判断出；
    ②若|
    a
    |=|
    b
    |，则
    a
    =
    b
    不一定成立；
    ③利用向量相等与平行四边形的定义即可得出；
    ④利用平行四边形的性质与向量相等即可得出；
    ⑤利用向量相等的定义即可判断出；
    ⑥
    a
    ∥
    b
    ，
    b
    ∥
    c
    ，则
    a
    ∥
    c
    ，取
    b
    =
    0
    时，
    a
    与
    c
    不一定共线．
    解答： 解：①两个向量相等，则它们的起点相同，终点相同，不一定正确；
    ②若|
    a
    |=|
    b
    |，方向不同，故
    a
    =
    b
    不一定成立；
    ③若
    AB
    =
    DC
    ，则四边形ABCD是平行四边形，正确；
    ④平行四边形ABCD中，一定有
    AB
    =
    DC
    ，正确；
    ⑤若
    m
    =
    n
    ，
    n
    =
    k
    ，则
    m
    =
    k
    ，正确；
    ⑥
    a
    ∥
    b
    ，
    b
    ∥
    c
    ，则
    a
    ∥
    c
    ，取
    b
    =
    0
    时，
    a
    与
    c
    不一定共线．
    其中不正确的命题的个数为1．
    故选：？．
    点评：本题考查了向量相等的意义、向量共线定理，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    关于向量的命题：
    ①零向量与任何向量平行；
    ②平行向量就是共线向量；
    ③平面内不共线的两个向量可以用来表示此平面内的任何向量；
    ④向量
    a
    在
    b
    方向上的投影也是向量．
    其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x＞1，则函数f（x）=x+1+
    1
    x-1
    的最小值为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列选项中，p是q的必要不充分条件的是（　　）
    A、p：a+c＞b+dq：a＞b且c＞d
    B、p：x=1q：x=x2
    C、p：a+bi（a，b∈R）是纯虚数q：a=0
    D、p：f（x）=x3+2x2+mx+1在R上单调递增q：m≥
    4
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列式子不正确的是（　　）
    A、（sin2x）′=2cos2x
    B、
    ∫
    1
    0
    xdx    =1
    C、
    ∫
    1
    0
    e2xdx=
    1
    2
    （e2-1）
    D、(
    sinx
    x
    )′=
    xcosx-sinx
    x2
    E、
    ∫
    1
    0
    e2xdx=
    1
    2
    e2x
    |
    1
    0
    =
    1
    2
    （e2-1），C正确；
    对于D，利用商的求导法则，正确．
    故选B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知一个角α终边上的一点坐标为（200，200），则cosα=（　　）
    A、
    1
    2
    B、
    		2
    2
    C、
    		3
    2
    D、0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列四个函数中，在（0，+∞）上为增函数的是（　　）
    A、f（x）=3-x
    B、f（x）=x2-3
    C、f（x）=
    1
    x
    D、f（x）=-x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    两条异面直线指的是（　　）
    A、不同在某个平面内的两条直线
    B、分别在某两个平面内的两条直线
    C、既不平行又不相交的两条直线
    D、平面内的一条直线和平面外的一条直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

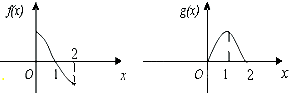    已知偶函数f（x）与奇函数g（x）的定义域都是（-2，2），它们在[0，2]上的图象如图所示，则使关于x的不等式f（x）•g（x）＞0成立的x的取值范围为（　　）
    A、（-2，-1）∪（1，2）
    B、（-1，0）∪（0，1）
    C、（-2，-1）∪（0，1）
    D、（-1，0）∪（1，2）

    查看答案和解析>>

    同步练习册答案