
���� ����һ�κ���������������ɵæգ�A��B��=0�������жϢ٣����A��B�����꣬��æգ�A��B���������жϢڣ����f��x���ĵ��������ò���ʽ�����ʣ��ɵæգ�A��B����2a�������жϢۣ���������ĵ����������¶�����æգ�A��B�����ɺ����˼�룬���ɵõ�t�ķ�Χ�������жϢܣ�
��� �⣺���ڢ٣�������f��x��=kx+b��k��0��ʱ��f�䣨x��=k��
�գ�A��B��=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$=$\frac{|k-k|}{|AB|}$=0���ʢ���ȷ��
���ڢڣ�������ɵ�A��1��1����B��2��5����f��x���ĵ���Ϊf�䣨x��=3x2-2x��
�ɵæգ�A��B��=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$=$\frac{|1-8|}{\sqrt{1+16}}$=$\frac{7}{\sqrt{17}}$��$\sqrt{3}$���ʢڲ���ȷ��
���ڢۣ�����f��x��=ax2+b�ĵ���Ϊf�䣨x��=2ax��
���Цգ�A��B��=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$=$\frac{|2a{x}_{1}-2a{x}_{2}|}{\sqrt{��{x}_{1}-{x}_{2}��^{2}+��a{{x}_{1}}^{2}-a{{x}_{2}}^{2}��^{2}}}$=$\frac{2a}{\sqrt{1+{a}^{2}��{x}_{1}+{x}_{2}��^{2}}}$��2a��
�ʢ���ȷ��
���ڢܣ���y=ex��y�䣨x��=ex��
��A��x1��y1����B��x2��y2��Ϊ����y=ex�����㣬��x1-x2=1��
�ɵæգ�A��B��=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$=$\frac{|{e}^{{x}_{1}}-{e}^{{x}_{2}}|}{\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{e}^{{x}_{1}}-{e}^{{x}_{2}}��^{2}}}$��
��t•�գ�A��B����1��������ɵ�t��$\sqrt{\frac{1}{��{e}^{{x}_{1}}-{e}^{{x}_{2}}��^{2}}+1}$��
��$\sqrt{\frac{1}{��{e}^{{x}_{1}}-{e}^{{x}_{2}}��^{2}}+1}$��1���ɵ�t��1���ʢܲ���ȷ��
�ʴ�Ϊ���٢ۣ�
���� ���⿼���¶������������ã���Ҫ���鵼�������ã������ߵ�б�ʣ�����ʽ���������Ľⷨ���������������������е�����״��⣮


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $\frac{{\sqrt{2}}}{2}$��$\sqrt{3}$ | C�� | $\frac{1}{2}$��$\sqrt{3}$ | D�� | $\frac{{\sqrt{2}}}{2}$��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | e |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
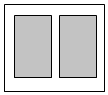 �������2016�괺������ʡ�ص��������Э�������п�����ѧ�Ծ������Ծ����д�С��ȵ������������������Ŀ����ͼ����Ӱ���֣��������������֮��Ϊ720cm2�����ܿհĿ���Ϊ4cm������֮����з�հĿ���Ϊ2cm�����Ծ��ĸߺͿ��ֱ�Ϊxcm��ycm��
�������2016�괺������ʡ�ص��������Э�������п�����ѧ�Ծ������Ծ����д�С��ȵ������������������Ŀ����ͼ����Ӱ���֣��������������֮��Ϊ720cm2�����ܿհĿ���Ϊ4cm������֮����з�հĿ���Ϊ2cm�����Ծ��ĸߺͿ��ֱ�Ϊxcm��ycm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
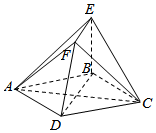 ��ͼ���ı���ABCDΪ���Σ�EB��ƽ��ABCD��EF��BD��EF=$\frac{1}{2}$BD��
��ͼ���ı���ABCDΪ���Σ�EB��ƽ��ABCD��EF��BD��EF=$\frac{1}{2}$BD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com