
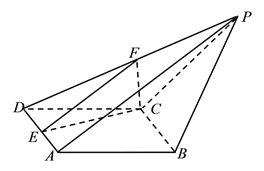
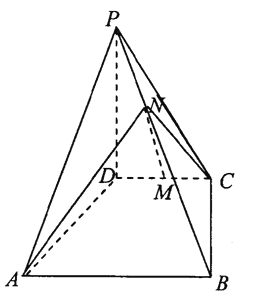
【题目】如图,在四棱锥![]() 中,
中,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(Ⅰ)运用几何法和坐标法两种方法进行证明可得结论.(Ⅱ)运用几何法和坐标法两种方法求解,利用坐标法求解时,在得到两平面法向量夹角余弦值的基础上,通过图形判断出二面角的大小,最后才能得到结论.
试题解析:
解法一:(Ⅰ)取![]() 中点
中点![]() ,连
,连![]() ,
,
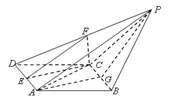
∵![]() ,
,
∴![]() ,
,
∵![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
, ![]() ,
,![]() ,
,
在![]() 中,根据余弦定理得
中,根据余弦定理得![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:(Ⅰ)∵![]() 是平行四边形,
是平行四边形,![]() ,
,
![]() ,∴
,∴![]() ,
,
∴![]() 是等边三角形,∵
是等边三角形,∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,∵
,∵![]() ∥
∥![]() ,
,
∴![]() .
.
以![]() 为坐标原点,建立如图所示的空间直角坐标系.
为坐标原点,建立如图所示的空间直角坐标系.
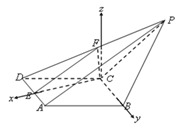
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,由
,由![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
由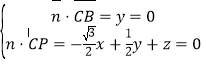 ,得
,得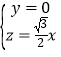 ,
,
令![]() ,则
,则![]() .
.
又![]() 是平面
是平面![]() 的法向量,
的法向量,
∴![]() ,
,
由图形知二面角![]() 为钝角,
为钝角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 与曲线
与曲线![]() 、
、![]() 分别交于点
分别交于点![]() (且
(且![]() 均异于原点
均异于原点![]() )当
)当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是梯形,
是梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 上一点,且
上一点,且![]() (
(![]() ).
).
(1)若![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求异面直线
,求异面直线![]() 与直线
与直线![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国政府实施“互联网+”战略以来,手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式,“一机在手,走遍天下”的时代已经到来。在某著名的夜市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“市场购物用手机支付与年龄有关”?
的把握认为“市场购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件
为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
|
|
|
|
|
|
|
|
|
|
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 24 | ||
合计 | 100 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,若
,若![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在抛物线
在抛物线![]() 上,是否存在直线
上,是否存在直线![]() 与椭圆交于
与椭圆交于![]() ,使得
,使得![]() 的中点
的中点![]() 落在直线
落在直线![]() 上,并且与抛物线
上,并且与抛物线![]() 相切,若直线
相切,若直线![]() 存在,求出
存在,求出![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com