
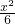 和y=|log2x|的图象的交点有且只有一个;
和y=|log2x|的图象的交点有且只有一个;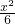 -|log2x|,通过零点存在定理研究函数有几个零点,即可得出两函数有几个交点;
-|log2x|,通过零点存在定理研究函数有几个零点,即可得出两函数有几个交点; )与(
)与( ,+∞)上是增函数,在(-
,+∞)上是增函数,在(- ,
, )是减函数,故函数存在极大值f(-
)是减函数,故函数存在极大值f(- )>0,极小值f(
)>0,极小值f( )<0,故函数有三个零点;
)<0,故函数有三个零点;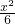 和y=|log2x|的图象的交点有且只有一个是错误的,可利用存在零点的条件f(a)f(b)<0来解决这个问题,两函数图象的交点的横坐标就是函数f(x)=
和y=|log2x|的图象的交点有且只有一个是错误的,可利用存在零点的条件f(a)f(b)<0来解决这个问题,两函数图象的交点的横坐标就是函数f(x)=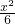 -|log2x|的零点,
-|log2x|的零点, >0,f(2)=-
>0,f(2)=- <0,f(4)=
<0,f(4)= >0,所以在直线x=1右侧,函数有两个零点.一个在(1,2)内,一个在(2,4)内,故函数f(x)=
>0,所以在直线x=1右侧,函数有两个零点.一个在(1,2)内,一个在(2,4)内,故函数f(x)=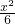 -|log2x|共有3个零点,即函数y=
-|log2x|共有3个零点,即函数y=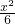 和y=|log2x|的图象有3个交点.
和y=|log2x|的图象有3个交点.

科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| a2+λb2 |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、8 | B、4 | C、2 | D、1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com