
数列{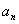 }的前n项和为
}的前n项和为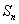 ,
,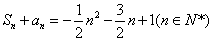 .
.
(Ⅰ)设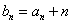 ,证明:数列
,证明:数列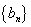 是等比数列;
是等比数列;
(Ⅱ)求数列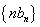 的前
的前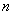 项和
项和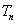 ;
;
(Ⅲ)若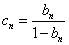 ,数列
,数列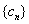 的前
的前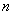 项和
项和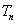 ,证明:
,证明: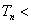
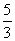 .
.
科目:高中数学 来源: 题型:
下列四个命题中,正确的有
①两个变量间的相关系数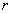 越小,说明两变量间的线性相关程度越低;
越小,说明两变量间的线性相关程度越低;
②命题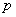 :“
:“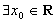 ,
,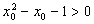 ”的否定
”的否定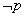 :“
:“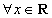 ,
,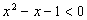 ”;
”;
③用相关指数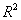 来刻画回归效果,若
来刻画回归效果,若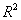 越大,则说明模型的拟合效果越好;
越大,则说明模型的拟合效果越好;
④若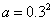 ,
,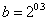 ,
,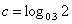 ,则
,则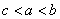 .
.
A.①③④ B.①④ C.③④ D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com