
分析 求出抛物线的焦点坐标,确定双曲线的c=2,结合抛物线的定义建立方程进行求解即可.
解答 解:抛物线y2=8x的焦点坐标F(2,0),
∵双曲线上一点$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的有共同的焦点F,
∴c=2,即a2+b2=4,
∵P到焦点F的距离为5,
∴$|{PF}|={x_0}+\frac{p}{2}={x_0}+2=5$,
∴${x_0}=3∴{y_0}^2=24$,
∴$\left\{{\begin{array}{l}{\frac{9}{a^2}-\frac{24}{b^2}=1}\\{{a^2}+{b^2}=4}\end{array}}\right.$,
∴a2=1,b2=3,
∴$e=\frac{c}{a}=2$,
故答案为:2
点评 本题主要考查双曲线离心率的计算,根据抛物线和双曲线的关系求出a,b,c是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
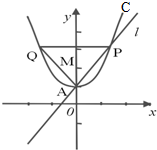 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 100 | C. | 36 | D. | 136 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com