练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】袋中装有9只球，其中标有数字1，2，3，4的小球各2个，标数字5的小球有1个.从袋中任取3个小球，每个小球被取出的可能性都相等，用表示取出的3个小球上的最大数字.

    （1）求取出的3个小球上的数字互不相同的概率；

    （2）求随机变量的分布列和期望.

    【答案】（1）；（2）的分布列见解析；期望是

    【解析】

    （1）先计算出一次取出的个小球上有两个数字相同的概率，然后用减去这个概率，求得取出的3个小球上的数字互不相同的概率.（2）所有可能的取值为：2，3，4，5，根据分类加法计数原理和古典概型概率计算公式，计算出分布列并求得数学期望.

    解:（1）一次取出的个小球上的数字互不相同的事件记为

    则为一次取出的个小球上有两个数字相同

    ∴

    （2）由题意可知所有可能的取值为：2，3，4，5

    ；；

    ；

    ∴的分布列为：

    2

    3

    4

    5

    则

    答：随机变量的期望是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：分别加以统计，得到如图所示的频率分布直方图.

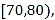
    （1）从样本中日平均生产件数不足60的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率；

    （2）规定日平均生产件数不少于80的为“生产能手”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？

    P（）

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    附：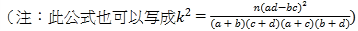

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的离心率为，且与抛物线交于，两点， （为坐标原点）的面积为．

    （1）求椭圆的方程；

    （2）如图，点为椭圆上一动点（非长轴端点），为左、右焦点，的延长线与椭圆交于点，的延长线与椭圆交于点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年，海南等8省公布了高考改革综合方案将采取“”模式，即语文、数学、英语必考，然后考生先在物理、历史中选择1门，再在思想政治、地理、化学、生物中选择2门为了更好进行生涯规划，甲同学对高一一年来的七次考试成绩进行统计分析，其中物理、历史成绩的茎叶图如图所示.

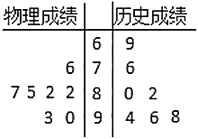
    （1）若甲同学随机选择3门功课，求他选到物理、地理两门功课的概率；

    （2）试根据茎叶图分析甲同学的物理和历史哪一学科成绩更稳定.（不需计算）

    （3）甲同学发现，其物理考试成绩（分）与班级平均分（分）具有线性相关关系，统计数据如下表所示，试求当班级平均分为50分时，其物理考试成绩.（计算，时精确到0.01）

    （分）

    57

    61

    65

    72

    74

    77

    84

    （分）

    76

    82

    82

    85

    87

    90

    93

    参考数据：，，，，，.

    参考公式：，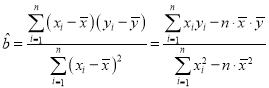

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程是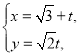（为参数），曲线的直角坐标方程为，将曲线上的点向下平移1个单位，然后横坐标伸长为原来的2倍，纵坐标不变，得到曲线．

    （1）求曲线和曲线的直角坐标方程；

    （2）若曲线和曲线相交于两点，求三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求曲线的普通方程和直线的直角坐标方程；

    （2）设点，若直线与曲线相交于、两点，求的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为抛物线的焦点，为圆上任意点，且最大值为.

    （1）求抛物线的方程；

    （2）若在抛物线上，过作圆的两条切线交抛物线于、，求中点的纵坐标的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴，取与直角坐标系相同的长度单位建立极坐标系.曲线的参数方程为，（为参数），曲线的极坐标方程为，且与交单的横坐标为.

    （1）求曲线的普通方程.

    （2）设为曲线与轴的两个交点，为曲线上不同于的任意一点，若直线与分别与交于两点，求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，函数，其中，是的一个极值点，且.

    （1）讨论的单调性

    （2）求实数和a的值

    （3）证明

    查看答案和解析>>

    同步练习册答案