
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了![]() 位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分
位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分![]() 分)制作的茎叶图如图所示:
分)制作的茎叶图如图所示:
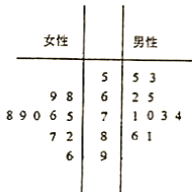
(1)分别计算男性打分的平均数和女性打分的中位数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民抽取
分)的市民抽取![]() 人,求有女性被抽中的概率.
人,求有女性被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.y=sin(2x+ ![]() )
)
B.y=sin( ![]() x+
x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
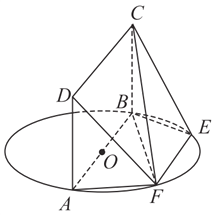
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com