
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
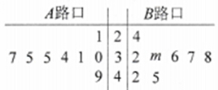
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知实数a,b,则“a>b”是“a2>b2”的必要不充分条件
B.“存在x0∈R,使得 ![]() ”的否定是“对任意x∈R,均有x2﹣1>0”
”的否定是“对任意x∈R,均有x2﹣1>0”
C.函数 ![]() 的零点在区间
的零点在区间 ![]() 内
内
D.设m,n是两条直线,α,β是空间中两个平面,若m?α,n?β,m⊥n,则α⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() cos2x+sin2(x+
cos2x+sin2(x+ ![]() ). (Ⅰ)求f(x)的最小正周期和单调递增区间;
). (Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[﹣ ![]() ,
, ![]() )时,求f(x)的取值范围.
)时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 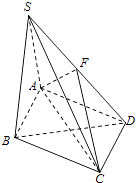
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子中装有三个编号分别为1,2,3的红球和三个编号分别为1,2,3的白球,三个红球按其编号分别记为a1 , a2 , a3 , 三个白球按其编号分别记为b1 , b2 , b3 , 袋中的6个球除颜色和编号外没有任何差异,现从袋中一次随机地取出两个球,
(1)列举所有的基本事件,并写出其个数;
(2)规定取出的红球按其编号记分,取出的白球按其编号的2倍记分,取出的两个球的记分之和为一次取球的得分,求一次取球的得分不小于6的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com