
【题目】若x=2是函数f(x)=x(x﹣m)2的极大值点,则m的值为( )
A.3
B.6
C.2或6
D.2
【答案】B
【解析】解:f(x)=x(x﹣m)2=x3﹣2mx2+m2x,则f′(x)=3x2﹣4mx+m2 ,
x=2是函数f(x)的极大值点,
f′(2)=0,12﹣8m+m2=0,解得m=2或6,
当m=2时,f(x)=x(x﹣2)2 , f′(x)=3x2﹣8x+4,
f′(x)>0,解得:x>2或x< ![]() ,
,
f′(x)<0,解得: ![]() <x<2,
<x<2,
∴f(x)的单调递增区间为:(﹣∞, ![]() ),(2,+∞),单调递减区间为:(
),(2,+∞),单调递减区间为:( ![]() ,2),
,2),
∴x= ![]() 是f(x)的极大值,x=2是f(x)的极小值;
是f(x)的极大值,x=2是f(x)的极小值;
当m=6时,f(x)=x(x﹣6)2 , f′(x)=3x2﹣24x+36,
f′(x)>0,解得:x>6或x<2,
f′(x)<0,解得:2<x<6,
∴f(x)的单调递增区间为:(﹣∞,2),(6,+∞),单调递减区间为:(2,6),
∴x=2是f(x)的极大值,x=6是f(x)的极小值;
所以m=6,
故答案选:B.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列![]() 同时满足下列条件:
同时满足下列条件:
①![]()
![]() ;②
;②![]()
![]() ;③
;③![]() 是
是![]() 的因数(
的因数(![]() ).
).
(Ⅰ)当![]() 时,写出数列
时,写出数列![]() 的前五项;
的前五项;
(Ⅱ)若数列![]() 的前三项互不相等,且
的前三项互不相等,且![]() 时,
时, ![]() 为常数,求
为常数,求![]() 的值;
的值;
(Ⅲ)求证:对任意正整数![]() ,存在正整数
,存在正整数![]() ,使得
,使得![]() 时,
时, ![]() 为常数.
为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E. 
(1)若D为AC的中点,证明:DE是⊙O的切线;
(2)若OA= ![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为( )
A.(0,+∞)
B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(0,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示,现从这20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)=( )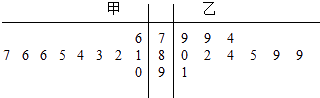
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
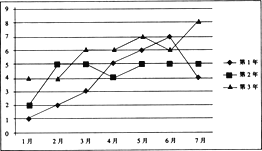
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 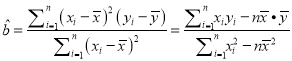 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组 ![]() .
.
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中点P(x,y),求点P落在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com