
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,满足
,满足![]() ,且线段
,且线段![]() 与
与![]() 互相平分(
互相平分(![]() 为原点),求
为原点),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)联立直线方程与抛物线方程,利用![]() 即可求解。
即可求解。
(2)由直线与抛物线相交可得:![]() ,由(1)可得
,由(1)可得![]()
![]() ,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C
,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C![]() ,利用
,利用![]() 得到
得到![]() ,即:
,即:![]()
![]() =-1,再将
=-1,再将![]()
![]() ,
,![]() 代入即可求得
代入即可求得![]() ,对
,对![]() 的范围分类,利用基本不等式即可得解。
的范围分类,利用基本不等式即可得解。
解:(1)法1:由![]() 得
得![]()
![]()
所以,所求的切线方程为![]()
法2:因为直线![]() 恒过(0,-4),所以由
恒过(0,-4),所以由![]() 得
得![]()
设切点为![]() ,由题可得,直线与抛物线在
,由题可得,直线与抛物线在![]() 轴下方的图像相切,
轴下方的图像相切,
则![]()
所以切线方程为![]() ,将坐标(0,-4)代入得
,将坐标(0,-4)代入得![]()
即切点为(8,-8),再将该点代入![]() 得,
得,![]()
所以,所求的切线方程为![]()
(2)由![]() 得
得![]()
![]() 且
且![]() ,
,![]()
![]()
所以![]() ,
,
因为线段OC与AB互相平分,所以四边形OACB为平行四边形
![]()
![]() ,即C
,即C![]()
由![]() 得,
得,![]() ,
,
法1:所以![]()
![]() =-1
=-1
又![]()
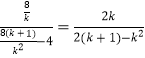 ,又
,又![]()
所以![]()
![]() ,所以
,所以![]()
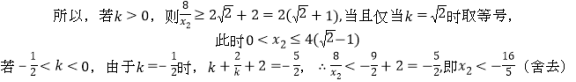
法2:因为![]()
![]()
又![]()
![]() ,即
,即![]()
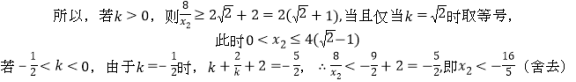


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A. B.
B.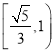
C.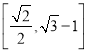 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,过点
中,过点![]() 的直线l的参数方程为
的直线l的参数方程为![]() (t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() 与曲线C相交于不同的两点M,N.
与曲线C相交于不同的两点M,N.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用![]() 种不同的颜色给图中的
种不同的颜色给图中的![]() 个格子涂色,每个格子涂一种颜色,要求最多使用
个格子涂色,每个格子涂一种颜色,要求最多使用![]() 种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,![]() 平面ABC,且
平面ABC,且![]() ,点M为线段VB的中点.
,点M为线段VB的中点.
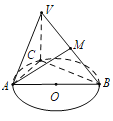
(1)求证:![]() 平面VAC;
平面VAC;
(2)若AB与平面VAC所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)已知某班共有![]() 人,记这
人,记这![]() 人生日至少有两人相同的概率为
人生日至少有两人相同的概率为![]() ,
,![]() ,将一年看作365天.
,将一年看作365天.
(i)求![]() 的表达式;
的表达式;
(ii)估计![]() 的近似值(精确到0.01).
的近似值(精确到0.01).
参考数值:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com