
【题目】已知抛物线E:![]() (
(![]() )的焦点为F,圆C:
)的焦点为F,圆C:![]() ,点
,点![]() 为抛物线上一动点.当
为抛物线上一动点.当![]() 时,
时,![]() 的面积为
的面积为![]() .
.
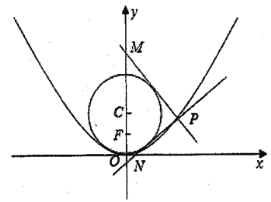
(1)求抛物线E的方程;
(2)若![]() ,过点P作圆C的两条切线分别交y轴于M,N两点,求
,过点P作圆C的两条切线分别交y轴于M,N两点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() ,由抛物线的定义求得
,由抛物线的定义求得![]() ,进而得到
,进而得到![]() ,再结合
,再结合![]() ,列出关于
,列出关于![]() 的方程,即可求得
的方程,即可求得![]() 的值,得到抛物线的方程;
的值,得到抛物线的方程;
(2)设![]() ,
,![]() ,且
,且![]() ,由圆心
,由圆心![]() 到直线PM当距离为1,利用点到直线的距离公式化简得
到直线PM当距离为1,利用点到直线的距离公式化简得![]() ,同理得到
,同理得到![]() ,进而得到
,进而得到![]() 为
为![]() 的两根,求得
的两根,求得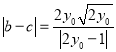 ,得到
,得到![]() 面积的表达式,利用均值不等式,即可求解.
面积的表达式,利用均值不等式,即可求解.
(1)由题意,抛物线E:![]() (
(![]() )的焦点为
)的焦点为![]() ,
,
圆![]() 的圆心C为
的圆心C为![]() ,
,
因为![]() ,由抛物线的定义可得
,由抛物线的定义可得![]() ,解得
,解得![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,即
,即![]() ,整理得
,整理得![]() ,
,
所以![]() 或
或![]()
解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以抛物线方程为
,所以抛物线方程为![]() .
.
(2)设![]() ,
,![]() ,且
,且![]() ,不妨设P在y轴右侧,
,不妨设P在y轴右侧,
故直线PM当方程为![]() ,即
,即![]() ,
,
由题设知,圆心![]() 到直线PM当距离为1,即
到直线PM当距离为1,即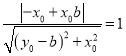 ,
,
化简上式得![]() ,同理可得
,同理可得![]() ,
,
由上可知![]() 为
为![]() 的两根,
的两根,
则![]() ,且
,且![]() ,
,
所以 ,
,
所以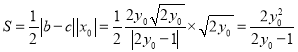 ,
,
设![]() ,
,![]()
![]() ,
,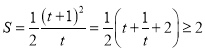 ,
,
所以![]() 面积的最小值
面积的最小值![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B.若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
C.在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
D.设从总体中抽取的样本为![]() 若记样本横、纵坐标的平均数分别为
若记样本横、纵坐标的平均数分别为![]() ,则回归直线
,则回归直线![]() 必过点
必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 内一点
内一点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 内切.
内切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)过点![]() 且不与坐标轴垂直的直线交曲线
且不与坐标轴垂直的直线交曲线![]() 于
于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,展现中国文化阴阳转化、对立统一的哲学理念.定义:图象能将圆的周长和面积同时等分成两部分的函数称为圆的一个“太极函数”,则下列命题正确的是___________.

(1)函数![]() 可以同时是无数个圆的“太极函数”;
可以同时是无数个圆的“太极函数”;
(2)函数![]() 可以是某个圆的“太极函数”;
可以是某个圆的“太极函数”;
(3)若函数![]() 是某个圆的“太极函数”,则函数
是某个圆的“太极函数”,则函数![]() 的图象一定是中心对称图形;
的图象一定是中心对称图形;
(4)对于任意一个圆,其“太极函数”有无数个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() 且满足
且满足![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(2)若方程![]() 有实数根
有实数根![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点,设正数
的一个不动点,设正数![]() 为函数
为函数![]() 的一个不动点,且
的一个不动点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com