Question

7．已知函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{2}\sqrt{{x^2}+1}，x≥0}\\{-ln（1-x），x＜0}\end{array}}$，若函数F（x）=f（x）-kx有且只有两个零点，则k的取值范围为（$\frac{1}{2}$，1）．

Answer 1

分析 求出双曲线的渐近线方程，y=-ln（1-x）在x=0处的切线方程，通过图象观察，即可得出结论．

解答 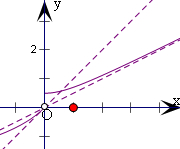解：由题意，x≥0，f（x）=$\frac{1}{2}$$\sqrt{1+{x}^{2}}$，
为双曲线4y²-x²=1在第一象限的部分，
渐近线方程为y=$\frac{1}{2}$x；
由y=-ln（1-x），
可得y′=$\frac{1}{1-x}$=1，可得x=0，
即y=-ln（1-x）在x=0处的切线方程为y=x，
此时函数F（x）=f（x）-kx有且只有1个零点，
若函数F（x）=f（x）-kx有且只有两个零点，
则k的取值范围为（$\frac{1}{2}$，1），
故答案为：（$\frac{1}{2}$，1）．

点评 本题考查函数的零点，考查导数知识的运用，考查学生分析解决问题的能力，以及数形结合的思想方法，知识综合性强．