练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某单位有男职工600名，女职工400人，在单位想了解本单位职工的运动状态，根据性别采取分层抽样的方法从全体职工中抽取100人，调查他们平均每天运动的时间（单位：小时），统计表明该单位职工平均每天运动的时间范围是[0，2]．若规定平均每天运动的时间不少于1小时的为“运动达人”，低于1小时的为“非运动达人”．根据调查的数据，按性别与是否为运动达人进行统计，得到如下2×2列联表．
    运动时间
    性别    		运动达人非运动达人合计
    男36
    女26
    合计100
    （Ⅰ）请根据题目信息，将2×2列联表中的数据补充完整，并通过计算判断能否在犯错误概率不超过0.025的前提下认为性别与是否为运动达人有关；
    （Ⅱ）将此样本的频率估计为总体的概率，随机调查该单位的3名男职工，设调查的3人中运动达人的人数为随机变量X，求X的分布列和数学期望E（X）及方差D（X）．
    附表及公式：
    　P（K2≥k0）　0.150.10　0.05　0.025　0.010　
    　k0　2.0722.706　3.841　　5.0246.635
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

    分析 （I）计算K2，根据临界值表作出结论；
    （II）分别计算X=0，1，2，3时的概率得出分布列，根据分布列得出数学期望和方差．

    解答 解：（I）由题意，该单位根据性别采取分层抽样的方法抽取的100人中，有60人为男职工，40人为女职工，据此2×2列联表中的数据补充如下．


    运动时间
    性别    		运动达人非运动达人合计
    男362460
    女142640
    合计5050100
    …（2分）
    由表中数据得观测值K2=$\frac{100×（36×26-14×24）^{2}}{60×40×50×50}$=6＞5.024，
    所以在犯错误概率不超过0.025的前提下，可以认为性别与是否为运动达人有关．…（5分）
    （2）随机调查一名男生，则这名男生为运动达人的概率为P=$\frac{36}{60}$=$\frac{3}{5}$．
    X的可能取值为0，1，2，3．
    ∴P（X=0）=（1-$\frac{3}{5}$）3=$\frac{8}{125}$，P（X=1）=C31（$\frac{3}{5}$）（1-$\frac{3}{5}$）2=$\frac{36}{125}$，
    P（X=2）=C32（$\frac{3}{5}$）2（1-$\frac{3}{5}$）=$\frac{54}{125}$，P（X=3）=（$\frac{3}{5}$）3=$\frac{27}{125}$．
    ∴X的分布列为：
    X0123
    P$\frac{8}{125}$$\frac{36}{125}$$\frac{54}{125}$$\frac{27}{125}$
    E（X）=3×$\frac{3}{5}$=$\frac{9}{5}$．D（X）=3×$\frac{3}{5}$×$\frac{2}{5}$=$\frac{18}{25}$．…（12分）

    点评 本题考查了独立性检验的应用，离散型随机变量的分布列、数学期望、方差的求法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知数列{an}的通项公式为an=3n-50，则当n等于（　　）时，Sn取得最小值？
    A．16B．17C．18D．16或17

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列是x和y之间的一组数据
    x0123
    y1357
    则y关于x的线性回归方程为y=bx+a，对应的直线必过点（　　）
    A．（2，2）B．（$\frac{3}{2}，2$）C．（ $\frac{3}{2}，4$）D．（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数f（x）=$\sqrt{3}$sin（2x+$\frac{π}{3}$），其中x∈R，下列结论中正确的是（　　）
    A．f（x）是最小正周期为π的偶函数
    B．f（x）的一条对称轴是 $x=\frac{π}{3}$
    C．f（x）的最大值为2
    D．将函数$y=\sqrt{3}sin2x$的图象向左平移$\frac{π}{6}$个单位得到函数f（x）的图象

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{2}\sqrt{{x^2}+1}，x≥0}\\{-ln（1-x），x＜0}\end{array}}$，若函数F（x）=f（x）-kx有且只有两个零点，则k的取值范围为（$\frac{1}{2}$，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．sin315°的值为（　　）
    A．-$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{\sqrt{2}}{2}$D．-$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．曲线f（x）=$\frac{1}{2}$x2+lnx的切线的斜率的最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．在直角坐标系xOy中，L的参数方程$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数），C的参数方程为$\left\{\begin{array}{l}{x=1+2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数）．
    （1）求L和C的普通方程；
    （2）已知P（0，1），L与C交于A、B两点，求|PA||PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

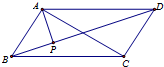    2．如图，在平行四边形ABCD中，AP⊥BD，垂足为P，且AP=2，则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8．

    查看答案和解析>>

    同步练习册答案