【题目】已知复数z＝
，（m∈R，i是虚数单位）．
（1）若z是纯虚数，求m的值；
（2）设
是z的共轭复数，复数
＋2z在复平面上对应的点在第一象限，求m的取值范围．
【答案】(1) 
(2) 
【解析】试题分析：（1）化简z＝1－2m＋(2m＋1)i，若z是纯虚数，只需1－2m＝0且2m＋1≠0即可；
（2）求得
1－2m－(2m＋1)i，得
＋2z=3－6m＋(2m＋1)i，只需
即可.
试题解析：
（1）z＝
＝
＝1－2m＋(2m＋1)i．
因为z是纯虚数，所以1－2m＝0且2m＋1≠0，
解得m＝
．
（2）因为
是z的共轭复数，所以＝1－2m－(2m＋1)i．
所以＋2z＝1－2m－(2m＋1)i＋2[1－2m＋(2m＋1)i]
＝3－6m＋(2m＋1)i．
因为复数＋2z在复平面上对应的点在第一象限，
所以
解得－＜m＜，即实数m的取值范围为(－，)．
点睛:形如
的数叫复数,其中a叫做复数的实部,b叫做复数的虚部.
当
时复数
为实数,
当
时复数
为虚数,
当
时复数
为纯虚数.
一线名师提优试卷系列答案科目：高中数学 来源： 题型：
【题目】椭圆
的经过中心的弦称为椭圆的一条直径，平行于该直径的所有弦的中点的轨迹为一条线段，称为该直径的共轭直径，已知椭圆的方程为
.
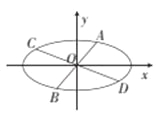
（1）若一条直径的斜率为
，求该直径的共轭直径所在的直线方程；
（2）若椭圆的两条共轭直径为
和
，它们的斜率分别为
，证明：四边形
的面积为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中， 
为正三角形，平面
底面
，底面
为梯形， 
， 
， 
， 
， 
，点
在棱
上，且
．
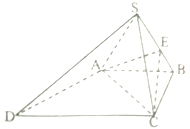
求证：（1）平面
平面
；
（2）求证： 
平面
；
（3）求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
定义域为
，若对于任意的
，都有
，且
时，有
.
（1）判断并证明函数
的奇偶性；
（2）判断并证明函数
的单调性；
（3）设
，若
，对所有
，
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（x+1）e2x ， g（x）=aln（x+1）+ 
x2+（3﹣a）x+a（a∈R）．
（1）当a=9，求函数y=g（x）的单调区间；
（2）若f（x）≥g（x）恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知圆C经过点A(1，3) ，B(4，2)，且圆心在直线l：x－y－1＝0上．
（1）求圆C的方程；
（2）设P是圆D：x2＋y2＋8x－2y＋16＝0上任意一点，过点P作圆C的两条切线PM，PN，M，N为切点，试求四边形PMCN面积S的最小值及对应的点P坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
