
分析 已知ABC-A1B1C1是直三棱柱,取BC的中点0,连接A0,NM,BM,BM∥NO,BC∥NM,那么AN和NO所成角即为BM与AN所成角.求出边长,利用余弦定理求解角的大小.
解答 解:∵M,N分别是A1B1,A1C1的中点,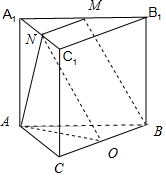
取BC的中点0,连接AO,NM,BM,
∴BM∥NO,BC∥NM且BC=2NM,
那么AN和NO所成角即为BM与AN所成角.
∵设BC=CC1=CA=2,∠BCA=90°,ABC-A1B1C1是直三棱柱,
∴AO=$\sqrt{5}$,AN=$\sqrt{5}$,BM=NO=$\sqrt{6}$
cos∠ANO=$\frac{A{N}^{2}+N{O}^{2}-A{O}^{2}}{2AN•NO}$=$\frac{\sqrt{30}}{10}$
sin∠ANO=$\sqrt{1-co{s}^{2}∠ANO}=\frac{\sqrt{70}}{10}$.
故答案为$\frac{\sqrt{70}}{10}$.
点评 本题考查两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 若f(x1)=f(x2),则x1+x2=kπ | |
| B. | f(x)的图象关于点$({-\frac{3π}{8},0})$对称 | |
| C. | f(x)的图象关于直线$x=\frac{5π}{8}$对称 | |
| D. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得$g(x)=\sqrt{2}sin({2x+\frac{3π}{4}})$的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow m∥\overrightarrow n$ | B. | $\overrightarrow m⊥\overrightarrow n$ | ||
| C. | $\overrightarrow m$与$\overrightarrow n$既不平行也不垂直 | D. | 以上情况均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15π | B. | 17π | C. | 19π | D. | 21π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com