
| A. | $\overrightarrow m∥\overrightarrow n$ | B. | $\overrightarrow m⊥\overrightarrow n$ | ||
| C. | $\overrightarrow m$与$\overrightarrow n$既不平行也不垂直 | D. | 以上情况均有可能 |
分析 利用向量垂直与数量积的关系即可得出.
解答 解:∵向量$\overrightarrow m$同时垂直于$\overrightarrow a$、$\overrightarrow b$,非零向量$\overrightarrow a$,$\overrightarrow b$不共线,
∴$\overrightarrow{m}•\overrightarrow{n}$=2$\overrightarrow{m}•\overrightarrow{a}$+3$\overrightarrow{m}•\overrightarrow{b}$=0,
∴$\overrightarrow{m}$$⊥\overrightarrow{n}$.
故选:B.
点评 本题考查了向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
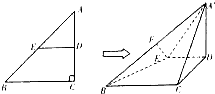 如图,在△ABC中,∠C=90°,AC=BC,D,E分别是AC,AB的中点,现将△ABC沿DE折成直二面角A′-DE-B,连接A′B,A′C,F是A′B的中点.
如图,在△ABC中,∠C=90°,AC=BC,D,E分别是AC,AB的中点,现将△ABC沿DE折成直二面角A′-DE-B,连接A′B,A′C,F是A′B的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com