
一个多面体的直观图及三视图如图所示,其中 M , N 分别是 AF、BC 的中点,
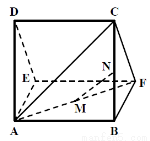

(1)求证: MN // 平面 CDEF ;
(2)求二面角 A-CF-B 的余弦值;
(1)详见解析;(2) .
.
【解析】
试题分析:(1)由三视图知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=4,DE=CF= ,∠CBF=90°,由此能证明MN∥平面CDEF.(2)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A-CF-B的余弦值.
,∠CBF=90°,由此能证明MN∥平面CDEF.(2)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A-CF-B的余弦值.
(2)(法二):以EA,AB,AD所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A-CF-B的余弦值.
试题解析: 解(1)证明:由三视图知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=4,DE=CF= ,
,
,连结BE, M在BE上,连结CE
(2)方法一:作BQ⊥CF于Q,连结AQ,
面BFC⊥面ABFE,面ABFE∩面BFC=BF,
AB?面ABFE,AB⊥BF,
∴AB⊥面BCF,
CF?面BCF,∴AB⊥CF,BQ⊥CF,AB∩BQ=B,
∴CF⊥面ABQ,AQ?面ABQ,
AQ⊥CF,∴∠AQB为所求的二面角的平面角,(8分)
在Rt△ABQ中,tan∠AQB= ,
,
∴cos∠AQB= ,
,
∴二面角A-CF-B的余弦值为 .
.
(2)方法二:以EA,AB,AD所在直线为x轴,y轴,z轴建立空间直角坐标系,

所以
面CBF法向量为

设面ACF法向量为 ,
,

取 ,所以
,所以
考点:1.用空间向量求平面间的夹角;2.直线与平面平行的判定.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
从0,1,3,4,5,6六个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位数,这样的三位数共有( )
A、24个 B、36个 C、48个 D、54个
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:选择题
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x,若方程ax+a-f(x)=0(a>0)恰有三个不相等的实数根,则实数a的取值范围是( )
A、(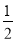 ,1) B、[0,2] C、(1,2) D、[1,+∞)
,1) B、[0,2] C、(1,2) D、[1,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:选择题
某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为k:5:3,现用分层抽样方法抽出一个容量为120的样本,已知A种型号产品共抽取了24件,则C种型号产品抽取的件数为( )
A、24 B、30 C、36 D、40
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:选择题
在 中,内角 A、B、C 的对边分别是 a、b、c ,若
中,内角 A、B、C 的对边分别是 a、b、c ,若 ,则B=( )
,则B=( )
A.30° B.60° C.120° D.150°
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试理科数学试卷(解析版) 题型:填空题
已知等差数列 中,
中, 为其前
为其前 项和.若
项和.若 ,
, ,则公差
,则公差 _______;数列
_______;数列 的前______项和最大.
的前______项和最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com