练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个均匀的正方体玩具，各个面上分别写有1，2，3，4，5，6，将这个玩具先后抛掷2次，求：
    （1）朝上的一面数相等的概率；
    （2）朝上的一面数之和小于5的概率．

    【答案】
    （1）解：基本事件共6×6=36个：

    （1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（5，5），（5，6），（6，1），（6，2），（6，3），（6，4），（6，5），（6，6）．

    朝上一面数相等的有6个，则朝上的一面数相等的概率P=


    （2）解：由（1）知，朝上的一面数之和小于5有6个，

    故朝上的一面数之和小于5的概率P=


    【解析】（1）列举出所有36个基本事件，由古典概型的概率计算公式可求；（2）由（1）可知朝上一面数之和小于5包含的基本事件数，由古典概型概率计算公式可求；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

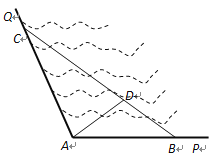
    【题目】如图所示， 是某海湾旅游区的一角，其中，为了营造更加优美的旅游环境，旅游区管委会决定在直线海岸和上分别修建观光长廊和AC，其中是宽长廊，造价是元/米， 是窄长廊，造价是元/米，两段长廊的总造价为120万元，同时在线段上靠近点的三等分点处建一个观光平台，并建水上直线通道（平台大小忽略不计），水上通道的造价是元/米．

    (1) 若规划在三角形区域内开发水上游乐项目，要求的面积最大，那么和的长度分别为多少米？

    (2) 在(1)的条件下，建直线通道还需要多少钱？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

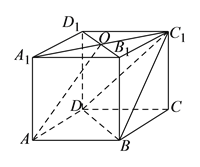
    【题目】在四棱柱中，底面，底面为菱形，为与交点，已知，．

    （I）求证：平面．

    （II）在线段上是否存在一点，使得平面，如果存在，求的值，如果不存在，请说明理由．

    （III）设点在内（含边界），且，求所有满足条件的点构成的图形，并求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的方程2x2﹣（ +1）x+m=0的两根为sinθ和cosθ，θ∈（0，π）．求：
    （1）m的值；
    （2）+ 的值；
    （3）方程的两根及此时θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sin2x（x∈R）图象上所有的点向左平移 个单位长度，所得图象的函数解析式为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是圆心为的圆上的动点，点， 为坐标原点，线段的垂直平分线交于点.

    （1）求动点的轨迹的方程；

    （2）过原点作直线交（1）中的轨迹于点，点在轨迹上，且，点满足，试求四边形的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列为公差不为的等差数列， 为前项和， 和的等差中项为，且．令数列的前项和为．

    （1）求及；

    （2）是否存在正整数成等比数列？若存在，求出所有的的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆： 的离心率为， 为椭圆的右焦点， ， .

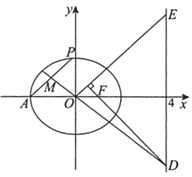
    （Ⅰ）求椭圆的方程；

    （Ⅱ）设为原点， 为椭圆上一点， 的中点为，直线与直线交于点，过且平行于的直线与直线交于点．求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是等差数列，其前项和为， 是等比数列，且， ， ．

    （1）求数列与的通项公式；

    （2）求的值．

    查看答案和解析>>

    同步练习册答案