
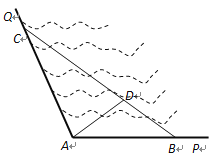
����Ŀ����ͼ��ʾ�� ![]() ��ij������������һ�ǣ�����
��ij������������һ�ǣ�����![]() ��Ϊ��Ӫ��������������λ�������������ί�������ֱ�ߺ���
��Ϊ��Ӫ��������������λ�������������ί�������ֱ�ߺ���![]() ��
��![]() �Ϸֱ����۹ⳤ��
�Ϸֱ����۹ⳤ��![]() ��AC������
��AC������![]() �ǿ����ȣ������
�ǿ����ȣ������![]() Ԫ/�ף�
Ԫ/�ף� ![]() ��խ���ȣ������
��խ���ȣ������![]() Ԫ/�ף����γ��ȵ������Ϊ120��Ԫ��ͬʱ���߶�
Ԫ/�ף����γ��ȵ������Ϊ120��Ԫ��ͬʱ���߶�![]() �Ͽ�����
�Ͽ�����![]() �����ȷֵ�
�����ȷֵ�![]() ����һ���۹�ƽ̨������ˮ��ֱ��ͨ��
����һ���۹�ƽ̨������ˮ��ֱ��ͨ��![]() ��ƽ̨��С���Բ��ƣ���ˮ��ͨ���������
��ƽ̨��С���Բ��ƣ���ˮ��ͨ���������![]() Ԫ/�ף�
Ԫ/�ף�
(1) ���滮��������![]() �����ڿ���ˮ��������Ŀ��Ҫ��
�����ڿ���ˮ��������Ŀ��Ҫ��![]() ����������ô
����������ô![]() ��
��![]() �ij��ȷֱ�Ϊ�����ף�
�ij��ȷֱ�Ϊ�����ף�
(2) ��(1)�������£���ֱ��ͨ��![]() ����Ҫ����Ǯ��
����Ҫ����Ǯ��
���𰸡���1��![]() ��AC�ij��ȷֱ�Ϊ750��1500�ף�2��
��AC�ij��ȷֱ�Ϊ750��1500�ף�2��![]() ��Ԫ
��Ԫ
�������������������1����![]() ��Ϊ
��Ϊ![]() �ף�
�ף� ![]() ��Ϊ
��Ϊ![]() �ף��������
�ף��������![]() ����
����![]() ����ʾ���,���û�������ʽ�ɵý��ۣ���2������������������
����ʾ���,���û�������ʽ�ɵý��ۣ���2������������������![]() ��ʾΪ
��ʾΪ![]() ��������������������ģ���Ĺ�ϵ�ɵý��.
��������������������ģ���Ĺ�ϵ�ɵý��.
�����������1����![]() ��Ϊ
��Ϊ![]() �ף�
�ף� ![]() ��Ϊ
��Ϊ![]() �ף��������
�ף��������![]() ��
��
��![]() ��
��
![]()
![]()
![]()
![]() =
=![]()
![]()
���ҽ���![]() ����
����![]() ʱ�Ⱥų�����
ʱ�Ⱥų�����
���Ե�![]() ��������ʱ��
��������ʱ�� ![]() ��AC�ij��ȷֱ�Ϊ750��1500��
��AC�ij��ȷֱ�Ϊ750��1500��
![]() ��
��
��![]()
��![]()
![]()
![]()
![]()
![]() ��
��
![]() Ԫ
Ԫ
���ԣ���ˮ��ͨ��![]() ����Ҫ
����Ҫ![]() ��Ԫ��
��Ԫ��
�ⷨ������![]() �У�
�У� ![]()
![]()
![]()
��![]() ��
�У� ![]()
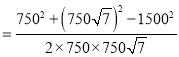
![]()
��![]() ��
�У� ![]()
![]() =
=![]()
![]() Ԫ
Ԫ
���ԣ���ˮ��ͨ��![]() ����Ҫ
����Ҫ![]() ��Ԫ��
��Ԫ��
�ⷨ������AΪԭ�㣬��ABΪ![]() �Ὠ��ƽ��ֱ������ϵ����
�Ὠ��ƽ��ֱ������ϵ����![]() ��
�� ![]()
![]() ,��
,��![]() ����
����![]()
��![]() �����
�����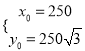 �� ����
�� ����![]()
���ԣ� ![]()
![]()
![]() Ԫ
Ԫ
���ԣ���ˮ��ͨ��![]() ����Ҫ
����Ҫ![]() ��Ԫ��
��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�a��b��c�ֱ��ǡ�A����B����C�ĶԱ߳�����֪a��b��c�ɵȱ����У���a2��c2=ac��bc��
��1�����A�Ĵ�С��
��2���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��![]() ��������
��������![]() �ཻ�ڲ�ͬ����
�ཻ�ڲ�ͬ����![]() ��
��![]() ����Բ
����Բ![]() �����ڵ�
�����ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �е���
���
(1) ��![]() ����������
���������Σ�![]() ������ԭ�㣩����������εı߳���
������ԭ�㣩����������εı߳���
(2) ��![]() ����ֱ��
����ֱ��![]() �ķ�����
�ķ�����
(3) ����![]() �������ۣ�����д������������ֱ��
�������ۣ�����д������������ֱ��![]() ��������ֱ��д�����ۣ���
��������ֱ��д�����ۣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x�����㣺f��x��= ![]() ����f��x+2��=f��x����g��x��=
����f��x+2��=f��x����g��x��= ![]() ����f��x��=g��x��������[��5��1]�ϵ�����ʵ��֮��Ϊ�� ��
����f��x��=g��x��������[��5��1]�ϵ�����ʵ��֮��Ϊ�� ��
A.��5
B.��6
C.��7
D.��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+�գ���x��R������A��0���أ�0��0���գ� ![]() ����ͼ����x��Ľ����У�������������֮��ľ���Ϊ
����ͼ����x��Ľ����У�������������֮��ľ���Ϊ ![]() ����ͼ����һ����ߵ�ΪM��
����ͼ����һ����ߵ�ΪM�� ![]() ��3����
��3����
��1����f��x���Ľ���ʽ��
��2���ȰѺ���y=f��x����ͼ������ƽ�� ![]() ����λ���ȣ�Ȼ���ٰ�����ͼ���ϸ���ĺ������쳤��ԭ����2���������겻�䣩���õ�����y=g��x����ͼ����д������y=g��x���Ľ���ʽ��
����λ���ȣ�Ȼ���ٰ�����ͼ���ϸ���ĺ������쳤��ԭ����2���������겻�䣩���õ�����y=g��x����ͼ����д������y=g��x���Ľ���ʽ��
��3���ڣ�2���������£����ܴ���x0��[�� ![]() ��
�� ![]() ]��ʹ�ò���ʽg��x0��+2��log3m��������ʵ��m����Сֵ��
]��ʹ�ò���ʽg��x0��+2��log3m��������ʵ��m����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=4cos2x��4 ![]() sinxcosx����С������Ϊ�У���0����
sinxcosx����С������Ϊ�У���0����
��1������ֵ��
��2����f��x���Ķ�����Ϊ[�� ![]() ��
�� ![]() ]����f��x�������ֵ����Сֵ����Ӧ��x��ֵ��
]����f��x�������ֵ����Сֵ����Ӧ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��
������![]() ����
����![]() ������[-1,2]�ϵ�ȡֵ��Χ��
������[-1,2]�ϵ�ȡֵ��Χ��
������������![]() ��
�� ![]() ���������
���������![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ȵ���������ߣ��������Ϸֱ�д��1��2��3��4��5��6�����������Ⱥ�����2�Σ���
��1�����ϵ�һ������ȵĸ��ʣ�
��2�����ϵ�һ����֮��С��5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com