
【题目】已知定义在R上的函数f(x)满足:f(x)= ![]() ,且f(x+2)=f(x),g(x)=
,且f(x+2)=f(x),g(x)= ![]() ,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为( )
,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为( )
A.﹣5
B.﹣6
C.﹣7
D.﹣8
【答案】C
【解析】解:∵f(x)= ![]() ,且f(x+2)=f(x),
,且f(x+2)=f(x),
∴f(x﹣2)﹣2= ![]() ;
;
又g(x)= ![]() ,
,
∴g(x)=2+ ![]() ,
,
∴g(x﹣2)﹣2= ![]() ,
,
当x≠2k﹣1,k∈Z时,
上述两个函数都是关于(﹣2,2)对称,;
由图象可得:方程f(x)=g(x)在区间[﹣5,1]上的实根有3个,
x1=﹣3,x2满足﹣5<x2<﹣4,x3满足0<x3<1,x2+x3=﹣4;
∴方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为﹣7.
所以答案是;C.
【考点精析】关于本题考查的函数的零点与方程根的关系,需要了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]() .
.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是
的定义域是![]() ,对于以下四个命题:
,对于以下四个命题:
(1) 若![]() 是奇函数,则
是奇函数,则![]() 也是奇函数;
也是奇函数;
(2) 若![]() 是周期函数,则
是周期函数,则![]() 也是周期函数;
也是周期函数;
(3) 若![]() 是单调递减函数,则
是单调递减函数,则![]() 也是单调递减函数;
也是单调递减函数;
(4) 若函数![]() 存在反函数
存在反函数![]() ,且函数
,且函数![]() 有零点,则函数
有零点,则函数![]() 也有零点.
也有零点.
其中正确的命题共有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,an+1=2an+1,b1=4,bn﹣bn﹣1=an+1(n≥2).
(1)求证:数列{an+1}是等比数列;
(2)求数列{an},{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 是定义在(﹣1,1)上的奇函数,且
是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)确定函数的解析式;
(2)证明函数f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
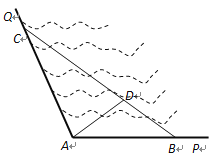
【题目】如图所示, ![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米, ![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+sin(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)的最大值和最小值;
(3)若f(α)= ![]() ,求sin 2α的值.
,求sin 2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的方程2x2﹣( ![]() +1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
+1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
(1)m的值;
(2)![]() +
+ ![]() 的值;
的值;![]()
(3)方程的两根及此时θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com