
【题目】已知函数f(x)=sinx+sin(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)的最大值和最小值;
(3)若f(α)= ![]() ,求sin 2α的值.
,求sin 2α的值.
【答案】
(1)解:∵ ![]() =
= ![]() ∴函数f(x)=sin x+sin(x+
∴函数f(x)=sin x+sin(x+ ![]() )的最小正周期是2π.
)的最小正周期是2π.
(2)解:∵x∈R,﹣1≤sinx≤1
![]() =
= ![]()
∴f(x)的最大值为 ![]() ,最小值为
,最小值为 ![]()
(3)解:∵f(α)=sinα+sin(α+ ![]() )=sinα+cosα=
)=sinα+cosα= ![]()
∴(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+sin2α= ![]()
∴sin2α= ![]() ﹣1=
﹣1= ![]()
【解析】(1)根据诱导公式可求出函数的解析式,推断f(x)的最小正周期是2π(2)依上问f(x)=2sinx,根据正弦函数的性质推断f(x)的最大值是2,最小值是﹣2.(3)把α代入函数式,两边平方可得答案.
【考点精析】解答此题的关键在于理解二倍角的正弦公式的相关知识,掌握二倍角的正弦公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:f(x)= ![]() ,且f(x+2)=f(x),g(x)=
,且f(x+2)=f(x),g(x)= ![]() ,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为( )
,则方程f(x)=g(x)在区间[﹣5,1]上的所有实根之和为( )
A.﹣5
B.﹣6
C.﹣7
D.﹣8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4cos2x﹣4 ![]() sinxcosx的最小正周期为π(>0).
sinxcosx的最小正周期为π(>0).
(1)求的值;
(2)若f(x)的定义域为[﹣ ![]() ,
, ![]() ],求f(x)的最大值与最小值及相应的x的值.
],求f(x)的最大值与最小值及相应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
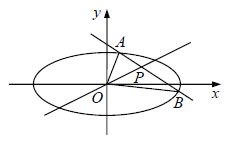
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式![]() 的解集为
的解集为![]() ;命题q:函数
;命题q:函数![]() 为增函数.命题r:a满足
为增函数.命题r:a满足![]() .
.
(1)若p∨q是真命题且p∧q是假题.求实数a的取值范围.
(2)试判断命题¬p是命题r成立的一个什么条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一枚质地均匀的骰子,连续投掷两次,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是7的结果有多少种?
(3)向上的点数之和是7的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com