
【题目】设函数f(x)=4cos2x﹣4 ![]() sinxcosx的最小正周期为π(>0).
sinxcosx的最小正周期为π(>0).
(1)求的值;
(2)若f(x)的定义域为[﹣ ![]() ,
, ![]() ],求f(x)的最大值与最小值及相应的x的值.
],求f(x)的最大值与最小值及相应的x的值.
【答案】
(1)解:函数f(x)=4cos2x﹣4 ![]() sinxcosx
sinxcosx
=4 ![]() ﹣4
﹣4 ![]()
![]() sin2ωx
sin2ωx
=2cos2ωx﹣2 ![]() sin2ωx+2
sin2ωx+2
=﹣4sin(2ωx﹣ ![]() )+2,
)+2,
又f(x)的最小正周期为T= ![]() =π,
=π,
所以=1
(2)解:∵f(x)=﹣4sin(2x﹣ ![]() )+2的定义域为[﹣
)+2的定义域为[﹣ ![]() ,
, ![]() ],即x∈[﹣
],即x∈[﹣ ![]() ,
, ![]() ],
],
∴2x∈[﹣ ![]() ,
, ![]() ],
],
2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
所以sin(2x﹣ ![]() )∈[﹣1,
)∈[﹣1, ![]() ];
];
所以当sin(2x﹣ ![]() )=﹣1时,f(x)取得最大值为﹣4×(﹣1)+2=6,此时x=﹣
)=﹣1时,f(x)取得最大值为﹣4×(﹣1)+2=6,此时x=﹣ ![]() ;
;
当sin(2x﹣ ![]() )=
)= ![]() 时,f(x)取得最小值为﹣4×
时,f(x)取得最小值为﹣4× ![]() +2=0,此时x=
+2=0,此时x= ![]()
【解析】(1)利用三角恒等变换化简函数f(x),再根据周期为π求出ω的值;(2)当x∈[﹣ ![]() ,
, ![]() ]时,利用正弦函数的图象与性质求出f(x)的最大、最小值以及对应的x值.
]时,利用正弦函数的图象与性质求出f(x)的最大、最小值以及对应的x值.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知以
中,已知以![]() 为圆心的圆的方程为:
为圆心的圆的方程为: ![]() ,以
,以![]() 为圆心的圆的方程为:
为圆心的圆的方程为: ![]() .
.
(1)若过点![]() 的直线
的直线![]() 沿
沿![]() 轴向左平移3个单位,沿
轴向左平移3个单位,沿![]() 轴向下平移4个单位后,回到原来的位置,求直线
轴向下平移4个单位后,回到原来的位置,求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
: ![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,an+1=2an+1,b1=4,bn﹣bn﹣1=an+1(n≥2).
(1)求证:数列{an+1}是等比数列;
(2)求数列{an},{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
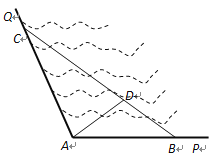
【题目】如图所示, ![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米, ![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
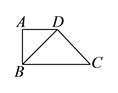
【题目】如图所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,构成四面体
,构成四面体![]() ,则在四面体
,则在四面体![]() 中,下列说法不正确的是( ).
中,下列说法不正确的是( ).
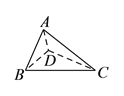
A. 直线![]() 直线
直线![]() B. 直线
B. 直线![]() 直线
直线![]()
C. 直线![]() 平面
平面![]() D. 平面
D. 平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+sin(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)的最大值和最小值;
(3)若f(α)= ![]() ,求sin 2α的值.
,求sin 2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求v与
垂直,求v与 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
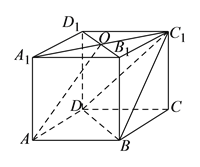
【题目】在四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.
(I)求证:![]() 平面
平面![]() .
.
(II)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,如果存在,求
,如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
(III)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]() ,求所有满足条件的点
,求所有满足条件的点![]() 构成的图形,并求
构成的图形,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为公差不为
为公差不为![]() 的等差数列,
的等差数列, ![]() 为前
为前![]() 项和,
项和, ![]() 和
和![]() 的等差中项为
的等差中项为![]() ,且
,且![]() .令
.令![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求![]() 及
及![]() ;
;
(2)是否存在正整数![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com