
分析 由已知利用模的等式两边平方得到|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,将所求平方利用此关系得到关于t的二次函数解析式,然后求最小值
解答 解:因为非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{5π}{6}$,且|$\overrightarrow{a}$|=|$\overrightarrow{a}+\overrightarrow{b}$|,
所以|$\overrightarrow{a}$|2=|$\overrightarrow{a}+\overrightarrow{b}$|2,所以|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,
则($\frac{|\overrightarrow{a}+t\overrightarrow{b}|}{|\overrightarrow{b}|}$)2=$\frac{{\overrightarrow{a}}^{2}+{t}^{2}{\overrightarrow{b}}^{2}+2t\overrightarrow{a}•\overrightarrow{b}}{{\overrightarrow{b}}^{2}}$=t2-t+$\frac{1}{3}$=(t-$\frac{1}{2}$)2+$\frac{1}{12}$,
所以当t=$\frac{1}{2}$时,则$\frac{|\overrightarrow{a}+t\overrightarrow{b}|}{|\overrightarrow{b}|}$的最小值为$\sqrt{\frac{1}{12}}=\frac{\sqrt{3}}{6}$;
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查了向量的数量积公式的运用以及向量的平方与模的平方相等的运用,关键是将所求转化为关于t 的二次函数求最值.属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
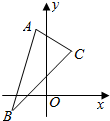 已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
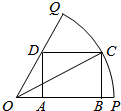 如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{3}$ | B. | -6 | C. | 6 | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com