
 的图象恰好经过k个格点,则称函数
的图象恰好经过k个格点,则称函数 为k阶格点函数. 已知下列函数:①
为k阶格点函数. 已知下列函数:① ;②
;② ;③
;③ ;④
;④ .则其中为一阶格点函数的序号为 .(写出所有正确命题的序号)
.则其中为一阶格点函数的序号为 .(写出所有正确命题的序号)科目:高中数学 来源:不详 题型:解答题
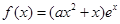 ,其中e是自然数的底数,
,其中e是自然数的底数, .
. 时,解不等式
时,解不等式 ;
; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解;
在[k,k+1]上有解; 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ),映射
),映射 满足:①当
满足:①当 时,
时, ;②任取
;②任取 ,若
,若 ,则有
,则有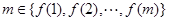 .则称映射
.则称映射 是一个“优映射”.例如:用表1表示的映射
是一个“优映射”.例如:用表1表示的映射 是一个“优映射”.
是一个“优映射”.| i | 1 | 2 | 3 |
| f(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| f(i) | | 3 | | |
 是一个“优映射”,请把表2补充完整.
是一个“优映射”,请把表2补充完整. 是“优映射”,且方程
是“优映射”,且方程 的解恰有6个,则这样的“优映射”的个数是 .
的解恰有6个,则这样的“优映射”的个数是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 cm的小正方形,折成一个容积是
cm的小正方形,折成一个容积是 的无盖长方体铁盒,试写出用
的无盖长方体铁盒,试写出用 表示
表示 的函数关系式,并指出它的定义域。
的函数关系式,并指出它的定义域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com