
| A. | 2012 | B. | 4024 | C. | 2014 | D. | 4025 |
分析 设 f(x)=$\frac{1}{x-1}$,g(x)=2sinπx,此题是求以上两个函数的交点的横坐标的和的问题.从x=2开始,在每个周期上,f(x) 和 g(x)都有两个交点,在区间[2,2014]上,函数g(x) 共有1006个周期,因此和函数f(x)有2012个交点,因此在区间[-2012,0]上也有2012个交点.m是两个函数的一个交点的横坐标,则2-m也是两个函数的一个交点的横坐标,因为一共有2012对这样的交点,故所有根之和等于2×2012=4024
解答 解:函数f(x)=2(x-1)sinπx-1的零点,
即方程2(x-1)sinπx-1=0的根,
即方程2sinπx=$\frac{1}{x-1}$的根,
由f(x)=$\frac{1}{x-1}$,g(x)=2sinπx的图象均关于(1,0)点对称,
且在g(x)=2sinπx的每一个周期上均有两个交点,
故从x=2开始,在每个周期上,f(x) 和 g(x)都有两个交点,
在区间[2,2014]上,函数g(x) 共有1006个周期,因此和函数f(x)有2012个交点,
因此在区间[-2012,0]上也有2012个交点,
且对每一个交点,相对于(1,0)中心对称的点也是两个函数的交点.
而每对这样的交点之和为2,即若m是两个函数的一个交点的横坐标,则2-m也是两个函数的一个交点的横坐标,
因为一共有2012对这样的交点.
所以,在区间[-2012,2014]上,两个函数所有交点的横坐标的和为2012×2=4024,
故选:B
点评 本题考查了根的存在性及根的个数判断,以及函数与方程的思想,属于中档题


科目:高中数学 来源: 题型:解答题
 已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
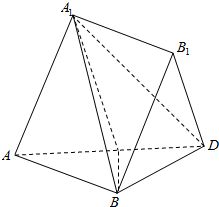 如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.
如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com