分析:由双曲线方程确定一条渐近线为y=2x,可得AB为圆直径且AB=2a,因椭圆与双曲线有公共焦点,得a
2-b
2=5.设C
1与y=2x在第一象限的交点为A(m,2m),代入C
1解出
m2=.再由对称性知直线y=2x被C
1截得的弦长,根据C
1恰好将线段AB三等分解出
m=,联解可得a
2,b
2的值,得到答案.
解答:解:由题意,C
2的焦点为(±
,0),一条渐近线方程为y=2x,
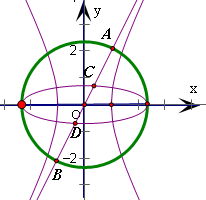
根据对称性可知以C
1的长轴为直径的圆交y=2x于A、B两点,满足AB为圆的直径且AB=2a
∵椭圆C
1与双曲线C
2有公共的焦点,
∴C
1的半焦距c=
,可得a
2-b
2=5,…①
设C
1与y=2x在第一象限的交点的坐标为A(m,2m),
代入C
1的方程,解得
m2=,…②
由对称性可得直线y=2x被C
1截得的弦长AB=2
m,
结合题意得2
m=
,所以
m=,…③
由②③联解,得a
2=11b
2…④
再联解①④,可得得a
2=5.5,b
2=0.5
故答案为:0.5
点评:本题给出双曲线与椭圆共焦点,在双曲线的渐近线与椭圆长轴为直径的圆相交所得的弦AB被椭圆三等分时,求椭圆的b2之值.着重考查了椭圆、双曲线的标准方程与简单几何性质与直线与圆等知识,属于中档题.




 已知椭圆C1:
已知椭圆C1: