
| A. | (0,2] | B. | $[\frac{1}{2},2]$ | C. | [2,+∞) | D. | $(0,\frac{1}{2}]∪[{2,+∞})$ |
分析 根据函数奇偶性和单调性之间的关系,进行转化,结合对数函数的运算性质,即可比较大小.
解答 解:∵f(x)是定义在R上的偶函数,
∴不等式$f({log_2}a)+f({log_{\frac{1}{2}}}a)≤2f(1)$,
等价为f(log2a)+f(-log2a)≤2f(1),
即2f(log2a)≤2f(1),f(log2a)≤f(1),
即f(|log2a|)≤f(1),
∵在区间[0,+∞)上单调递减,
∴|log2a|≥1,
即log2a≥1或log2a≤-1,
解得a≥2或0<a≤$\frac{1}{2}$,
故选:D.
点评 本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:选择题
已知在 中,
中, ,
, ,
, ,
, 是
是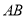 上的点,则
上的点,则 到
到 的距离的乘积的最大值为( )
的距离的乘积的最大值为( )
A.3 B.2 C. D.9
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnx | B. | y=x3 | C. | $y={(\frac{1}{2})^x}$ | D. | y=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )| A. | -8 | B. | $-\frac{1}{4}$ | C. | -2 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com