
分析 (Ⅰ)判断点(1,0),在椭圆内,交点设为M(x1,y1),N(x2,y2),表示出斜率,利用平方差法推出斜率关系,得到a2=2b2,利用点在椭圆是得到$\frac{2}{a^2}+\frac{1}{b^2}=1$,解得a2,b2,求出椭圆C的方程.
(Ⅱ)联立y=k(x-1)与椭圆C,利用弦长公式,表示出△AMN面积,化简求解即可.
解答 解:(Ⅰ)由题可得直线过点(1,0),在椭圆内,
所以与椭圆一定相交,
交点设为M(x1,y1),N(x2,y2),
则$k=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$,OP斜率为$\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$,
所以$\frac{y_1^2-y_2^2}{x_1^2-x_2^2}=-\frac{1}{2}$,┅┅┅┅┅┅┅(3分)
又$\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1$,$\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1$,所以$\frac{x_1^2-x_2^2}{a^2}+\frac{y_1^2-y_2^2}{b^2}=0$,
所以a2=2b2,又$\frac{2}{a^2}+\frac{1}{b^2}=1$,解得a2=4,b2=2,
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$;┅┅┅┅┅┅┅(6分)
(Ⅱ)椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$;
椭圆C的右顶点为A(2,0),直线过点P(1,0),|AP|=1.
y=k(x-1)与椭圆C联立得:(1+2k2)x2-4k2x+2k2-4=0,┅┅┅┅┅┅┅(8分),
x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-4}{1+2{k}^{2}}$,y1-y2=k(x1-x2).
△AMN面积为:$\frac{1}{2}|AP|•|{y}_{1}-{y}_{2}|$=$\frac{1}{2}|{y_1}-{y_2}|=\frac{|k|}{2}|{x_1}-{x_2}|=\frac{|k|}{2}\frac{{\sqrt{8(2+3{k^2})}}}{{1+2{k^2}}}=\frac{{\sqrt{10}}}{3}$,
解得k=±1.┅┅┅┅┅┅┅(12分)
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,三角形的面积的解法,点到直线的距离公式,考查转化思想以及计算能力.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数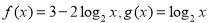 .
.
(1)当x∈[1,4]时,求函数 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式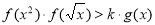 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
在 中,若
中,若 依次成等差数列,则( )
依次成等差数列,则( )
A.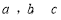 依次成等差数列
依次成等差数列
B.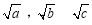 依次成等差数列
依次成等差数列
C.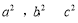 依次成等差数列
依次成等差数列
D.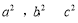 依次成等比数列
依次成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
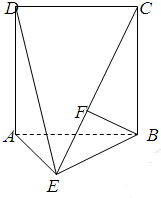 如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,F为CE上的点,且BF⊥平面ACE.
如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,F为CE上的点,且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,△ACB为等腰直角三角形,AC=BC,AC⊥BC,点E、F分别在BC上,且CE=BF,CM⊥AE,AE与MF的延长线相交于N点
如图1,△ACB为等腰直角三角形,AC=BC,AC⊥BC,点E、F分别在BC上,且CE=BF,CM⊥AE,AE与MF的延长线相交于N点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com