
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)由离心率可得![]() 关系,再将点
关系,再将点![]() 坐标代入,可得
坐标代入,可得![]() 间关系,又
间关系,又![]() ,解方程可得
,解方程可得![]() 的值;(II)由
的值;(II)由![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴,可判断直线
轴,可判断直线![]() 的斜率互为相反数,由两直线都过
的斜率互为相反数,由两直线都过![]() 点,由点斜式可写出直线方程.一一与椭圆方程联立,消去
点,由点斜式可写出直线方程.一一与椭圆方程联立,消去![]() 的值,可得一元二次方程,又
的值,可得一元二次方程,又![]() 点满足条件,可求得
点满足条件,可求得![]() 点的坐标,用
点的坐标,用![]() 表示.再由斜率公式可得直线
表示.再由斜率公式可得直线![]() 的斜率为定值.
的斜率为定值.
试题解析:
(Ⅰ) 因为椭圆![]() 的离心率为
的离心率为![]() , 且过点
, 且过点![]() ,
,
所以![]() ,
, ![]() .
.
因为![]() ,
,
解得![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)法1:因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对
对
称. 设直线![]() 的斜率为
的斜率为![]() , 则直线
, 则直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
设点![]() ,
, ![]() ,
,
由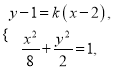 消去
消去![]() ,得
,得![]() . ①
. ①
因为点![]() 在椭圆
在椭圆![]() 上, 所以
上, 所以![]() 是方程①的一个根, 则
是方程①的一个根, 则![]() ,
,
所以![]() .
.
同理![]() .
.
所以![]() .
.
又![]() .
.
所以直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.
法2:设点![]() ,
,
则直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() , ①
, ①
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,②
,②
![]() . ③
. ③
由②得![]() , 得
, 得![]() , ④
, ④
同理由③得![]() , ⑤
, ⑤
由①④⑤得![]() ,
,
化简得![]() , ⑥
, ⑥
由①得![]() , ⑦
, ⑦
⑥![]() ⑦得
⑦得![]() .
.
②![]() ③得
③得![]() ,得
,得![]() .
.
所以直线![]() 的斜率为
的斜率为![]() 为定值.
为定值.
法3:设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,
则![]() ,
,
直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() ,
,
化简得![]() .
.
把![]() 代入上式, 并化简得
代入上式, 并化简得
![]() . (*)
. (*)
由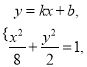 消去
消去![]() 得
得![]() , (**)
, (**)
则![]() ,
,
代入(*)得![]() ,
,
整理得![]() ,
,
所以![]() 或
或![]() .
.
若![]() , 可得方程(**)的一个根为
, 可得方程(**)的一个根为![]() ,不合题意.
,不合题意.
若![]() 时, 合题意.
时, 合题意.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若函数![]() ,
, ![]() 的最小值为-16,求实数
的最小值为-16,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵。某汽车经销商退出![]() 三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图。已知从
三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图。已知从![]() 三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元。现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆。以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率。
三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元。现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆。以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率。
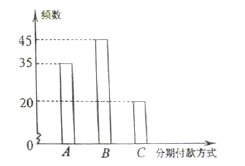
(Ⅰ)求甲乙两人采用不同分期付款方式的概率;
(Ⅱ)记![]() (单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求
(单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
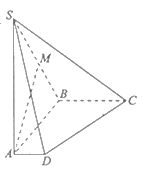
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的二面角的余弦值;
所成的二面角的余弦值;
(Ⅲ)设点![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)求![]() 的解析式;
的解析式;
(2)证明:函数![]() 在定义域上是增函数;
在定义域上是增函数;
(3)设![]() 是否存在正实数
是否存在正实数![]() 使得函数
使得函数![]() 在
在![]() 内的最小值为
内的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若存在,请说明理由.
的值;若存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
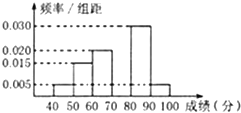
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).
(1)求成绩在[70,80)的频率和[70,80)这组在频率分布直方图中的纵坐标a的值;
(2)求这次考试平均分的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).
(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y=![]() 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;
(3)设h(x)=|af2(x)﹣![]() |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com