
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() 在区间
在区间![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,求证:在区间
时,求证:在区间![]() 至少存在一个
至少存在一个![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据二次函数![]() 在区间
在区间![]() 上单调递减得出
上单调递减得出![]() ,进而可求得实数
,进而可求得实数![]() 的取值范围;
的取值范围;
(2)由题意得出![]() 对任意的
对任意的![]() 恒成立,利用参变量分离法得出
恒成立,利用参变量分离法得出![]() ,求出函数
,求出函数![]() 在
在![]() 上的最大值,即可得出实数
上的最大值,即可得出实数![]() 的取值范围;
的取值范围;
(3)利用反证法,假设对任意的![]() ,均有
,均有![]() ,根据题意得出
,根据题意得出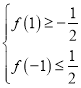 ,推出矛盾即可.
,推出矛盾即可.
(1)当![]() 时,
时,![]() ,该二次函数的图象开口向上,对称轴为直线
,该二次函数的图象开口向上,对称轴为直线![]() ,
,
由于函数![]() 在
在![]() 单调递减,则有
单调递减,则有![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由题可知![]() 在
在![]() 恒成立,则
恒成立,则![]() 且
且![]() ,
,
令![]() ,
,![]() ,则二次函数
,则二次函数![]() 在
在![]() 时单调递减,
时单调递减,
当![]() 时,函数
时,函数![]() 取得最大值,即
取得最大值,即![]() ,
,![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)由题可知![]() ,且
,且![]() ,函数开口向上,对称轴
,函数开口向上,对称轴![]() ,
,
则![]() 在
在![]() 单调递减,其值域为
单调递减,其值域为![]() ,
,
若不存在![]() 使得
使得![]() ,即对任意
,即对任意![]() 都有
都有![]() ,
,
即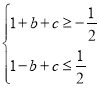 ,可得
,可得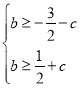 ,即
,即![]() ,与
,与![]() 矛盾.
矛盾.
故必存在![]() ,使得
,使得![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,短轴长为2,过定点
,短轴长为2,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间).
之间).
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ex+asinx,x∈(-π,+∞),下列说法正确的是( )
A.当a=1时,f(x)在(0,f(0))处的切线方程为2x-y+1=0
B.当a=1时,f(x)存在唯一极小值点x0且-1<f(x0)<0
C.对任意a>0,f(x)在(-π,+∞)上均存在零点
D.存在a<0,f(x)在(-π,+∞)上有且只有一个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为“中学数学联赛”选拔人才,分初赛和复赛两个阶段进行,规定:分数不小于本次考试成绩中位数的具有复赛资格,某校有900名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(1)求获得复赛资格应划定的最低分数线;
(2)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间
的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(3)从(2)抽取的7人中,选出4人参加全市座谈交流,设![]() 表示得分在
表示得分在![]() 中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在
中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在![]() 给予500元奖励,若该生分数在
给予500元奖励,若该生分数在![]() 给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
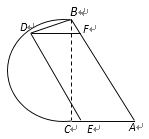
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是某校高三(1)班的一次数学知识竞赛成绩的茎叶图(图中仅列出![]() ,
,![]() 的数据)和频率分布直方图.
的数据)和频率分布直方图.
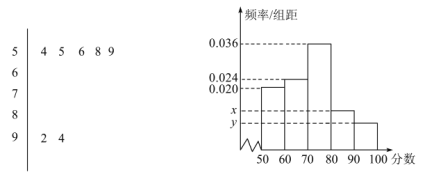
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求频率分布直方图中的![]() ;
;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们射击成绩的分布列如下表所示.
射手甲 | 射手乙 | ||||||
环数 |
|
|
| 环数 |
|
|
|
概率 |
|
|
| 概率 |
|
|
|
(1)若甲射手共有![]() 发子弹,一旦命中
发子弹,一旦命中![]() 环就停止射击,求他剩余
环就停止射击,求他剩余![]() 发子弹的概率;
发子弹的概率;
(2)若甲、乙两名射手各射击![]() 次,求
次,求![]() 次射击中恰有
次射击中恰有![]() 次命中
次命中![]() 环的概率;
环的概率;
(3)若甲、乙两名射手各射击![]() 次,记所得的环数之和为
次,记所得的环数之和为![]() ,求
,求![]() 的概率分布.
的概率分布.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com