
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 (单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现给出三个条件:①函数![]() 的图象关于直线
的图象关于直线![]() 对称;②函数
对称;②函数![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为![]() .从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
.从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
已知函数![]() (
(![]() ,
,![]() ),_____,_____.求函数
),_____,_____.求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面ABCD⊥平面PAD,AD∥BC,AB=BC![]() AD=1,∠APD=∠BAD=90°.
AD=1,∠APD=∠BAD=90°.
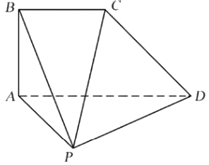
(1)求证:PD⊥PB;
(2)当PA=PD时,求三棱锥P﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,曲线C的参数方程为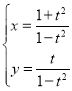 (t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(
(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(![]() )
)![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l交曲线C于A,B两点,交x轴于点P,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上位于
上位于![]() 轴两侧的不同两点
轴两侧的不同两点
(1)若![]() 在直线
在直线![]() 上,且使得以
上,且使得以![]() 为顶点的四边形恰为正方形,求该正方形的面积.
为顶点的四边形恰为正方形,求该正方形的面积.
(2)求过![]() 、
、![]() 的切线与直线
的切线与直线![]() 围成的三角形面积的最小值;
围成的三角形面积的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米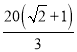 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
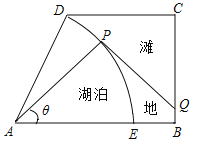
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com