
已知数列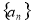 中,
中,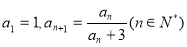 .
.
(1)求证: 是等比数列,并求
是等比数列,并求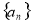 的通项公式
的通项公式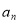 ;
;
(2)数列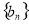 满足
满足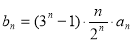 ,数列
,数列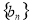 的前n项和为
的前n项和为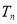 ,若不等式
,若不等式 对一切
对一切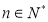 恒成立,求
恒成立,求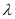 的取值范围.
的取值范围.
(1)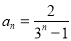 ;(2)
;(2)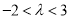 .
.
【解析】
试题分析:本题主要考查数列的证明、错位相减法、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,将已知的递推公式进行变形,转化出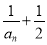 的形式来证明,还可以根据等比数列的定义来证明;第二问,将第一问得到的结论代入,先得到
的形式来证明,还可以根据等比数列的定义来证明;第二问,将第一问得到的结论代入,先得到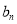 表达式,利用错位相减法,得到数列
表达式,利用错位相减法,得到数列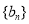 的前n项和
的前n项和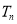 的值,再利用恒成立问题求
的值,再利用恒成立问题求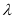 的值,在最后这一步,需要对n进行讨论,分奇数、偶数两种情况讨论.
的值,在最后这一步,需要对n进行讨论,分奇数、偶数两种情况讨论.
试题解析:(1)由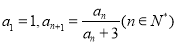 知,
知, ,
,
又 是以
是以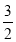 为首项,
为首项,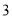 为公比的等比数列,
为公比的等比数列,
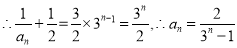 6分
6分
(2) ,
, 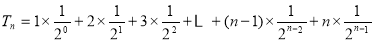
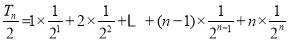 ,
,
两式相减得
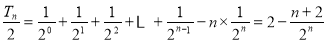 ,
,
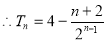 9分
9分
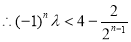 10分
10分
若n为偶数,则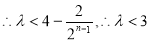 11分
11分
若n为奇数,则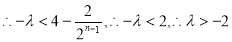 13分
13分
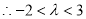 14分
14分
考点:数列的证明、错位相减法、恒成立问题.


科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二文科数学试卷(解析版) 题型:选择题
有两张卡片,一张的正反面分别写着数字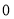 与
与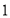 ,另一张的正反面分别写着数字
,另一张的正反面分别写着数字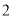 与
与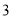 ,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
A.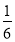 B.
B.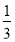 C.
C.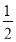 D.
D.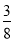
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知 、
、 是两条直线,
是两条直线, 、
、 是两个平面,给出下列命题:①若
是两个平面,给出下列命题:①若 ,
, ,则
,则 ;②若平面
;②若平面 上有不共线的三点到平面
上有不共线的三点到平面 的距离相等,则
的距离相等,则 ;③若
;③若 、
、 为异面直线,
为异面直线, ,
, ,
, ,
, ,则
,则 .其中正确命题的个数( )
.其中正确命题的个数( )
A. 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:选择题
设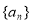 是等差数列,若
是等差数列,若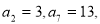 则数列
则数列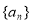 前8项和为( )
前8项和为( )
A.128 B.80 C.64 D.56
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:填空题
(坐标系与参数方程)已知曲线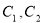 的极坐标方程分别为
的极坐标方程分别为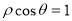 ,
,
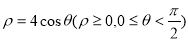 则曲线
则曲线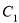 与
与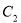 交点的极坐标为 .
交点的极坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com