
分析 (Ⅰ)判断P点的轨迹为以A、M为焦点的椭圆,设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,求出a,b,即可求解曲线W的方程.
(Ⅱ)设C(x1,y1)(x1y1≠0),E(x2,y2),则D(-x1,-y1),则直线CD的斜率为${k_{CD}}=\frac{y_1}{x_1}$,利用CE⊥CD,求出直线CE的斜率是${k_{CE}}=-\frac{x_1}{y_1}$,设直线CE的方程为y=kx+m,联立$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{3}+{y^2}=1}\end{array}}\right.$通过韦达定理,求出直线DE的方程为$y+{y_1}=\frac{y_1}{{3{x_1}}}(x+{x_1})$,顶点F(2x1,0).可得${k_2}=-\frac{y_1}{x_1}$,然后推出斜率比值.
解答 解:(Ⅰ)由题意知:点P在圆内且不为圆心,圆M:${({x-\sqrt{2}})^2}+{y^2}=12$及点$A({-\sqrt{2},0})$,动点P到圆M的距离与到A点的距离相等,故$|{PA}|+|{PM}|=2\sqrt{3}>2\sqrt{2}=|{AM}|$,
所以P点的轨迹为以A、M为焦点的椭圆,(2分)
设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,则$\left\{\begin{array}{l}2a=2\sqrt{3}\\ 2c=2\sqrt{2}\end{array}\right.⇒\left\{\begin{array}{l}a=\sqrt{3}\\ c=\sqrt{2}\end{array}\right.$,
所以b2=1,故曲线W的方程为$\frac{x^2}{3}+{y^2}=1$.(5分)
(Ⅱ)设C(x1,y1)(x1y1≠0),E(x2,y2),则D(-x1,-y1),则直线CD的斜率为${k_{CD}}=\frac{y_1}{x_1}$,又CE⊥CD,所以直线CE的斜率是${k_{CE}}=-\frac{x_1}{y_1}$,记$-\frac{x_1}{y_1}=k$,设直线CE的方程为y=kx+m,由题意知k≠0,m≠0,由$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{3}+{y^2}=1}\end{array}}\right.$得:(1+3k2)x2+6mkx+3m2-3=0.∴${x_1}+{x_2}=-\frac{6mk}{{1+3{k^2}}}$,∴${y_1}+{y_2}=k({x_1}+{x_2})+2m=\frac{2m}{{1+3{k^2}}}$,由题意知,x1≠x2,
所以${k_1}=\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}=-\frac{1}{3k}=\frac{y_1}{{3{x_1}}}$,(9分)
所以直线DE的方程为$y+{y_1}=\frac{y_1}{{3{x_1}}}(x+{x_1})$,令y=0,得x=2x1,即F(2x1,0).
可得${k_2}=-\frac{y_1}{x_1}$.(11分)
所以${k_1}=-\frac{1}{3}{k_2}$,即$\frac{k_1}{k_2}=-\frac{1}{3}$.(12分)
(其他方法相应给分)
点评 本题考查曲线轨迹方程的求法,直线与椭圆位置关系的综合应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | [0,1] | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
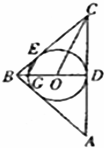 已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC=4
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC=4 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com