已知定直线l:x=1和定点M(t,0)(t∈R),动点P到M的距离等于点P到直线l距离的2倍.
(1)求动点P的轨迹方程,并讨论它表示什么曲线;
(2)当t=4时,设点P的轨迹为曲线C,过点M作倾斜角为θ(θ>0)的直线交曲线C于A、B两点,直线l与x轴交于点N.若点N恰好落在以线段AB为直径的圆上,求θ的值.
【答案】
分析:(1)设P(x,y),则由题意得
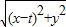
=2|x-1|,化简得3x
2-y
2+2(t-4)x+4-t
2=0,由此能够确定动点P的轨迹方程和它表示的曲线.
(2)当t=4时,C:
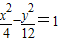
,M(4,0),N(1,0).由题意知 NA⊥NB,所以
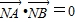
,设A(x
1,y
1),B(x
2,y
2),则当AB与x轴垂直时,不合题意;当AB与x轴不垂直时,设AB:y=k(x-4),代入双曲线方程并整理得:(3-k
2)x
2+8k
2x-16k
2-12=0,由此能够求出θ的值.
解答:解:(1)设P(x,y),则由题意得
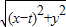
=2|x-1|,
化简得3x
2-y
2+2(t-4)x+4-t
2=0,
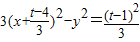
,…(4分)
当t=1时,化简得 y=±
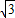
(x-1),表示两条直线;
当t≠1时,表示焦点在x轴上的双曲线.…(6分);
(2)当t=4时,C:
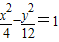
,M(4,0),N(1,0).
由题意知 NA⊥NB,
所以
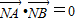
,…(8分);
设A(x
1,y
1),B(x
2,y
2),
则当AB与x轴垂直时,
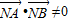
,不合题意;
当AB与x轴不垂直时,设AB:y=k(x-4),代入双曲线方程并整理得:
(3-k
2)x
2+8k
2x-16k
2-12=0,
由
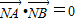
得(x
1-1)(x
2-2)+y
1y
2=0
所以 (k
2+1)x
1x
2-(4k
2+1)(x
1+x
2)+16k
2+1=0,
化简整理得k
2=

,
所以k=±
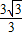
,…(11分)
经检验,均符合题意.
所以θ=30°或150°.…(12分)
点评:本题考查直线与圆锥曲线的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

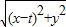 =2|x-1|,化简得3x2-y2+2(t-4)x+4-t2=0,由此能够确定动点P的轨迹方程和它表示的曲线.
=2|x-1|,化简得3x2-y2+2(t-4)x+4-t2=0,由此能够确定动点P的轨迹方程和它表示的曲线.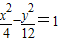 ,M(4,0),N(1,0).由题意知 NA⊥NB,所以
,M(4,0),N(1,0).由题意知 NA⊥NB,所以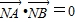 ,设A(x1,y1),B(x2,y2),则当AB与x轴垂直时,不合题意;当AB与x轴不垂直时,设AB:y=k(x-4),代入双曲线方程并整理得:(3-k2)x2+8k2x-16k2-12=0,由此能够求出θ的值.
,设A(x1,y1),B(x2,y2),则当AB与x轴垂直时,不合题意;当AB与x轴不垂直时,设AB:y=k(x-4),代入双曲线方程并整理得:(3-k2)x2+8k2x-16k2-12=0,由此能够求出θ的值.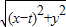 =2|x-1|,
=2|x-1|,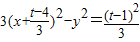 ,…(4分)
,…(4分)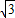 (x-1),表示两条直线;
(x-1),表示两条直线;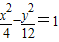 ,M(4,0),N(1,0).
,M(4,0),N(1,0).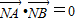 ,…(8分);
,…(8分);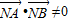 ,不合题意;
,不合题意;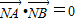 得(x1-1)(x2-2)+y1y2=0
得(x1-1)(x2-2)+y1y2=0 ,
,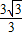 ,…(11分)
,…(11分)

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案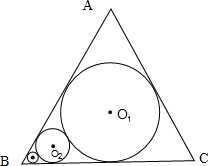 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.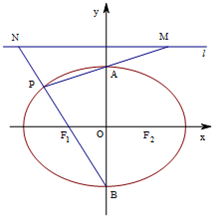 如图,焦点在x轴上的椭圆的离心率为
如图,焦点在x轴上的椭圆的离心率为