
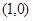 的直线与曲线
的直线与曲线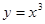 和
和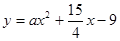 都相切,则
都相切,则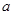 =_____.
=_____.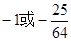 (只写对一个不给分)
(只写对一个不给分)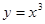 ⇒y'=3x2,设曲线y=x3上任意一点(x0,x03)处的切线方程为y-x03=3x02(x-x0),(1,0)代入方程得x0=0或x0="3" /2①当x0=0时,切线方程为y=0,则ax2+15 /4 x-9=0,△="(15" /4 )2-4a×(-9)=0⇒a="-25" /64
⇒y'=3x2,设曲线y=x3上任意一点(x0,x03)处的切线方程为y-x03=3x02(x-x0),(1,0)代入方程得x0=0或x0="3" /2①当x0=0时,切线方程为y=0,则ax2+15 /4 x-9=0,△="(15" /4 )2-4a×(-9)=0⇒a="-25" /64 

 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源:不详 题型:解答题
 在点
在点 的切线方程为
的切线方程为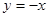
 的值;
的值;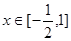 时,
时, 的图像与直线
的图像与直线 有两个不同的交点,求实数
有两个不同的交点,求实数 的取值范围;
的取值范围; ,不等式
,不等式 都成立.
都成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com