
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额![]() 元)、专业二等奖学金(奖金额
元)、专业二等奖学金(奖金额![]() 元)及专业三等奖学金(奖金额
元)及专业三等奖学金(奖金额![]() 元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校
元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
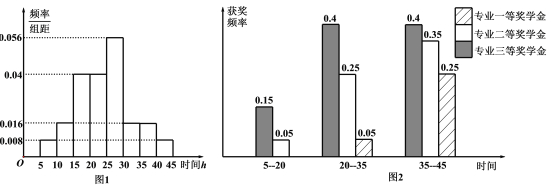
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生![]() 年获得的专业奖学金额为随机变量
年获得的专业奖学金额为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
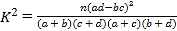
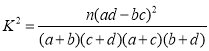
【答案】(Ⅰ)160人;(Ⅱ)有;(Ⅲ)见解析.
【解析】
(Ⅰ)根据频率之和为1,得到获得三等奖学金的频率,再由总人数得到答案;(Ⅱ)根据频率分布直方图和频率柱状图,填写好列联表,再计算出![]() 进行判断,得到答案;(Ⅲ)先得到
进行判断,得到答案;(Ⅲ)先得到![]() 可取的值,再分别求出其概率,根据数学期望的公式,得到答案.
可取的值,再分别求出其概率,根据数学期望的公式,得到答案.
![]() 获得三等奖学金的频率为:
获得三等奖学金的频率为:![]()
![]() ,
,
故这![]() 名学生获得专业三等奖学金的人数为
名学生获得专业三等奖学金的人数为![]() 人.
人.
![]() 每周课外学习时间不超过
每周课外学习时间不超过![]() 小时的“非努力型”学生有
小时的“非努力型”学生有![]()
其中获得一、二等奖学金学生有![]()
每周课外学习时间超过![]() 小时称为“努力型”学生有
小时称为“努力型”学生有![]() 人,
人,
其中获得一、二等奖学金学生有![]() 人,
人,
![]() 联表如图所示:
联表如图所示:
“非努力型”学生 | “努力型”学生 | 总计 | |
获得一二等奖学金学生 |
|
|
|
未获得一二等奖学金学生 |
|
|
|
总计 |
|
|
|
![]()
故有![]() 的把握认为获得一二等奖学金与学习“努力型”学生的学习时间有关;
的把握认为获得一二等奖学金与学习“努力型”学生的学习时间有关;
![]() 的可能取值为
的可能取值为![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 的分布列
的分布列
| 0 | 600 | 1500 | 3000 |
| 0.424 | 0.32 | 0.198 | 0.058 |
其期望为![]() 元.
元.


科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题:
①设![]() ,
,![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线;
的轨迹为双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为_____(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与两个定点
与两个定点![]() 距离的比是一个正数
距离的比是一个正数![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)当![]() 时得曲线
时得曲线![]() 的方程,把曲线
的方程,把曲线![]() 向左平移三个单位长度得到曲线
向左平移三个单位长度得到曲线![]() ,已知点
,已知点![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值;
的最小值;
(3)若直线![]() 与曲线
与曲线![]() 交于C、D两点,点
交于C、D两点,点![]() 是x轴上的点,使得
是x轴上的点,使得![]() 恒为定值,求点P的坐标和定值.
恒为定值,求点P的坐标和定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构用“10分制”调查了各阶层人士对某次国际马拉松赛事的满意度,现从调查人群中随机抽取16名,如图茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若满意度不低于9.5分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() 1,双曲线的一支上不同的三点A(x1,y1),B(6,
1,双曲线的一支上不同的三点A(x1,y1),B(6,![]() ),C(x2,y2)到焦点F(5,0)的距离成等差数列.
),C(x2,y2)到焦点F(5,0)的距离成等差数列.
(1)求m的值;
(2)试求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
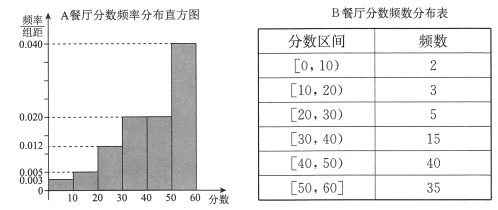
(Ⅰ)在抽样的100人中,求对![]() 餐厅评分低于30的人数;
餐厅评分低于30的人数;
(Ⅱ)从对![]() 餐厅评分在
餐厅评分在![]() 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在![]() 范围内的概率;
范围内的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上任意一点,
上任意一点,![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,过
的对称点,过![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com