
【题目】如图,在四棱锥E﹣ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3. 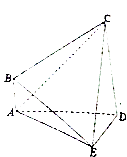
(1)求棱锥C﹣ADE的体积;
(2)在线段DE上是否存在一点P,使AF∥平面BCE?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)解:在Rt△ADE中,AE= ![]() =3
=3 ![]() ,
,
∴S△ADE= ![]() AEDE=
AEDE= ![]() ×3
×3 ![]() ×3=
×3= ![]()
![]() ,
,
∵CD⊥平面ADE,∴VC﹣ADE= ![]() CDS△ADE=
CDS△ADE= ![]() ×6×
×6× ![]()
![]() =9
=9 ![]()
(2)解:在线段DE上存在一点F,使AF∥平面BCE, ![]() =
= ![]() ,
,
下面给出证明:设F为线段DE上的一点,且 ![]() =
= ![]() ,
,
过F作FM∥CD交CE于点M,则FM= ![]() ,
,
∵CD⊥平面ADE,AB⊥平面ADE,
∴CD∥AB.又CD=3AB,
∴MF∥AB,MF=AB,
∴四边形ABMF是平行四边形,
∴AF∥BM,又AF平面BCE,BM平面BCE.
∴AF∥平面BCE.
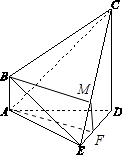
【解析】(1)在Rt△ADE中,AE= ![]() ,可得S△ADE=
,可得S△ADE= ![]() AEDE.由于CD⊥平面ADE,可得VC﹣ADE=
AEDE.由于CD⊥平面ADE,可得VC﹣ADE= ![]() CDS△ADE.(2)在线段DE上存在一点F,使AF∥平面BCE,
CDS△ADE.(2)在线段DE上存在一点F,使AF∥平面BCE, ![]() =
= ![]() ,设F为线段DE上的一点,过F作FM∥CD交CE于点M,由线面垂直的性质可得:CD∥AB.可得四边形ABMF是平行四边形,于是AF∥BM,即可证明AF∥平面BCE
,设F为线段DE上的一点,过F作FM∥CD交CE于点M,由线面垂直的性质可得:CD∥AB.可得四边形ABMF是平行四边形,于是AF∥BM,即可证明AF∥平面BCE
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】解答
(1)求函数f(x)= ![]() (x<﹣1)的最大值,并求相应的x的值.
(x<﹣1)的最大值,并求相应的x的值.
(2)已知正数a,b满足2a2+3b2=9,求a ![]() 的最大值并求此时a和b的值.
的最大值并求此时a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
xi(月) | 1 | 2 | 3 | 4 | 5 |
yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |

(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程 ![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克)
(参考公式: ![]() =
=  ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的左、右焦点分别为F1、F2 , P为C的右支上一点,且|PF2|=|F1F2|,则
的左、右焦点分别为F1、F2 , P为C的右支上一点,且|PF2|=|F1F2|,则 ![]() 等于( )
等于( )
A.24
B.48
C.50
D.56
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在三棱锥P﹣ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示. 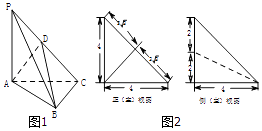
(1)证明:AD⊥BC;
(2)求三棱锥D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
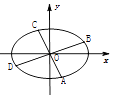
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]() .
. 
(1)求椭圆的标准方程;
(2)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若 ![]() . (i) 求
. (i) 求 ![]() 的最值;
的最值;
(ii) 求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,设命题p:函数y=ax在R上单调递增;命题q:不等式ax2﹣ax+1>0对x∈R恒成立,若p且q为假,p或q为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国古代著名的数学专著《九章算术》里有﹣段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里:驽马初日行九十七里,日减半里,良马先至齐,复还迎驽马,二马相逢, 问:需日相逢.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是一个面积较大的三角形,点P是△ABC所在平面内一点且 ![]() +
+ ![]() +2
+2 ![]() =
= ![]() ,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .
,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com