
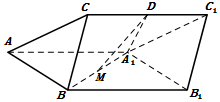
 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.分析 由已知可得${A_1}C={A_1}{C_1}=\sqrt{5}=AC$,CB⊥平面ABB1A1,取AA1中点F可得BC,BF,BB1两两互相垂直
以B为原点,BB1,BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1),$A(-1,\sqrt{3},0)$,${A_1}(1,\sqrt{3},0)$,C1(2,0,1),D(1,0,1),$M(\frac{1}{2},\frac{{\sqrt{3}}}{2},0)$,利用空间向量求解.
解答 解:∵A1D⊥CC1,且D为中点,AA1=A1D=2,∴${A_1}C={A_1}{C_1}=\sqrt{5}=AC$,
又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1,(1分)
又 BA∩BA1=B,∴CB⊥平面ABB1A1,(2分)
取AA1中点F,则BF⊥AA1,即BC,BF,BB1两两互相垂直,(3分)
以B为原点,BB1,BF,BC分别为x,y,z轴,建立空间直角坐标系如图所示,B1(2,0,0),C(0,0,1),$A(-1,\sqrt{3},0)$,${A_1}(1,\sqrt{3},0)$,C1(2,0,1),D(1,0,1),$M(\frac{1}{2},\frac{{\sqrt{3}}}{2},0)$(4分)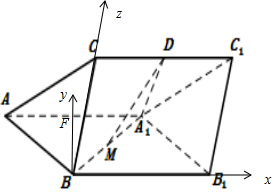
(I) $\overrightarrow{MD}=(\frac{1}{2},-\frac{{\sqrt{3}}}{2},1)$,设平面ABC的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}m•\overrightarrow{BA}=-x+\sqrt{3}y=0\\ m•\overrightarrow{BC}=z=0.\end{array}\right.$,取$m=(\sqrt{3},1,0)$,(6分)
∵$m•\overrightarrow{MD}=\frac{{\sqrt{3}}}{2}-\frac{{\sqrt{3}}}{2}+0=0$,∴$m⊥\overrightarrow{MD}$,(7分)
又MD?平面ABC,∴直线MD∥平面ABC.(8分)
(II) 设平面ACA1的法向量为n=(x1,y1,z1),$\overrightarrow{AC}=(1,-\sqrt{3},1),\overrightarrow{A{A_1}}=(2,0,0)$,
则$\left\{\begin{array}{l}n•\overrightarrow{AC}={x_1}-\sqrt{3}{y_1}+{z_1}=0\\ n•\overrightarrow{A{A_1}}={x_1}=0.\end{array}\right.$,取$n=(0,1,\sqrt{3})$,(10分)
又由(Ⅰ)知平面ABC的法向量为$m=(\sqrt{3},1,0)$,
设二面角B-AC-A1为θ,
∴$cosθ=|\frac{m•n}{|m|•|n|}|=\frac{1}{2•2}=\frac{1}{4}$,(11分)
∴二面角B-AC-A1的余弦值为$\frac{1}{4}$ (12分)
点评 本题考查了空间线面平行的判定,向量法二面角的余弦值,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
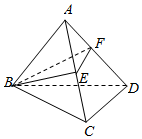 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com