
分析 将函数f(x)表示为分段函数形式,①根据奇偶性的定义进行判断,②利用周期性的定义进行排除,③结合三角函数的有界性进行求解,④求出函数的单调递增区间进行判断即可.
解答 解:当sinx≥0,即2kπ≤x≤2kπ+π,k∈Z,此时f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
当sinx<0,即2kπ-π≤x≤2kπ,k∈Z,此时f(x)=-sinx+cosx=$\sqrt{2}$cos(x+$\frac{π}{4}$),
①f(-x)=|sin(-x)|+cosx=|sinx|+cosx=f(x),则函数f(x)是偶函数,故①正确,
②f(x+$\frac{π}{2}$)=|sin(x+$\frac{π}{2}$)|+cos(x+$\frac{π}{2}$)=|cosx|-sinx≠f(x),则函数最小正周期为$\frac{π}{2}$错误,故②错误,
当2kπ≤x≤2kπ+π时,2kπ+$\frac{π}{4}$≤x+$\frac{π}{4}$≤2kπ+$\frac{5π}{4}$,此时$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
当2kπ-π≤x≤2kπ时,2kπ$-\frac{3π}{4}$≤x+$\frac{π}{4}$≤2kπ+$\frac{π}{4}$,此时$\sqrt{2}$cos(x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
综上f(x))∈[-1,$\sqrt{2}$],即函数的值域为[-1,$\sqrt{2}$],故③正确,
④作出函数f(x)的图象如图:函数单调递增的最大区间在函数f(x)=$\sqrt{2}$cos(x+$\frac{π}{4}$),
由2kπ-π≤x+$\frac{π}{4}$≤2kπ,k∈Z得2kπ-$\frac{5π}{4}$≤x≤2kπ-$\frac{π}{4}$,k∈Z
∵2kπ-π≤x≤2kπ,∴此时2kπ-π≤x≤2kπ-$\frac{π}{4}$,即此时函数的单调递增区间为[2kπ-π,2kπ-$\frac{π}{4}$],
当k=0时,单调递增区间为[-π,-$\frac{π}{4}$],此时区间长度为-$\frac{π}{4}$-(-π)=$\frac{3π}{4}$,
故④正确,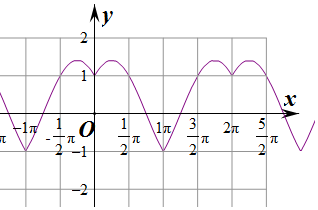
故答案为:①③④.
点评 本题主要考查与三角函数有关的命题的真假判断,利用绝对值的性质将函数表示成分段函数是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
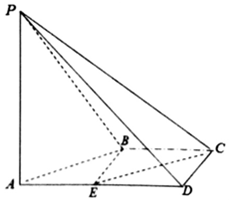 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$
如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
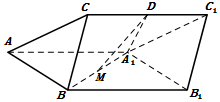 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com