【题目】已知函数f（x）=﹣alnx++x（a≠0）
（I）若曲线y=f（x）在点（1，f（1）））处的切线与直线x﹣2y=0垂直，求实数a的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）当a∈（﹣∞，0）时，记函数f（x）的最小值为g（a），求证：g（a）≤﹣e﹣4 ．

参考答案：

【答案】解：（I）由已知可知f（x）的定义域为{x|x＞0}
（x＞0）
根据题意可得，f′（1）=2×（﹣1）=﹣2
∴﹣a﹣2a2+1=﹣2
∴a=1或a=﹣
（II）∵=
①a＞0时，由f′（x）＞0可得x＞2a
由f′（x）＜0可得0＜x＜2a
∴f（x）在（2a，+∞）上单调递增，在（0，2a）上单调递减
②当a＜0时，
由f′（x）＞0可得x＞﹣a
由f′（x）＜0可得0＜x＜﹣a
∴f（x）在（﹣a，+∞）上单调递增，在（0，﹣a）上单调递减
（III）由（II）可知，当a∈（﹣∞，0）时，函数f（x）的最小值f（﹣a）
故g（a）=f（﹣a）=﹣aln（﹣a）﹣3a
则g′（a）=﹣ln（﹣a）﹣4
令g′（a）=0可得﹣ln（﹣a）﹣4=0
∴a=﹣e﹣4
当a变化时，g’（a），g（a）的变化情况如下表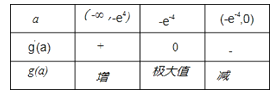

∴a=﹣e﹣4是g（a）在（﹣∞，0）上的唯一的极大值，从而是g（a）的最大值点
当a＜0时，=﹣e﹣4
∴a＜0时，g（a）≤﹣e﹣4 ．
【解析】（I）先求f（x）的定义域为{x|x＞0}，先对已知函数进行求导，由f′（1）=﹣2可求a
（II）由=通过比较﹣a与2a的大小解不等式f′（x）＞0，f′（x）＜0，从而可求函数的单调区间
（III）由（II）可知，当a∈（﹣∞，0）时，函数f（x）的最小值f（﹣a），结合已知可求a，然后结合已知单调性可求 ， 从而可证
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减)．

关闭