
分析 (Ⅰ)利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(Ⅱ)根据正弦函数的单调性,求得函数g(x)的单调增区间.
解答 解:(Ⅰ)∵f(x)=sinx,先把f(x)的横纵坐标各伸长2倍后,可得y=2sin$\frac{1}{2}$x的图象;
再向右平移$\frac{π}{3}$个单位,得到y=g(x)=2sin$\frac{1}{2}$(x-$\frac{π}{3}$)=2sin($\frac{x}{2}$-$\frac{π}{6}$)的图象,
∴函数g(x)的解析式为g(x)=2sin($\frac{x}{2}$-$\frac{π}{6}$).
(Ⅱ)令2kπ-$\frac{π}{2}$≤$\frac{x}{2}$-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得4kπ-$\frac{2π}{3}$≤x≤4kπ+$\frac{4π}{3}$,可得函数的增区间为[4kπ-$\frac{2π}{3}$,4kπ+$\frac{4π}{3}$],k∈Z.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.


科目:高中数学 来源: 题型:解答题
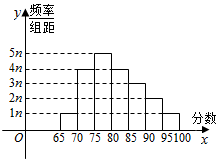 某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.
某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
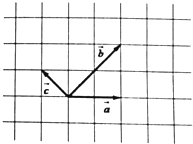 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
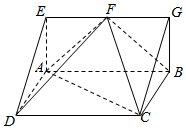 如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.
如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com