
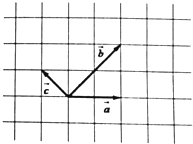
 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.分析 (1)根据向量加法和减法的运算法则进行求解即可.
(2)建立空间坐标系,求出向量的向量坐标,结合向量数量积的夹角关系进行求解即可.
解答 解:(1)根据向量加法的运算法则得以$\overrightarrow{a}$,$\overrightarrow{b}$向量所在的线段为边作平行四边形,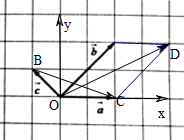
则对角线OD对应的向量为$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
连接AB,则$\overrightarrow{BC}$=$\overrightarrow{n}$=$\overrightarrow{a}$-$\overrightarrow{c}$;
(2)建立以O为坐标原点,的直角坐标系如图:
则$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(2,2),$\overrightarrow{c}$=(-1,1),
则$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$=(4,2),$\overrightarrow{n}$=$\overrightarrow{a}$-$\overrightarrow{c}$=(3,-1);
则$\overrightarrow{m}$•$\overrightarrow{n}$=4×3-1×2=12-2=10,
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{10}{\sqrt{16+4}•\sqrt{9+1}}=\frac{10}{\sqrt{20}•\sqrt{10}}=\frac{10}{10\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
则<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{π}{4}$,
则向量$\overrightarrow{m}$,$\overrightarrow{n}$的夹角是$\frac{π}{4}$.
点评 本题主要考查向量的四则运算以及向量数量积的应用,建立坐标系,利用坐标法是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
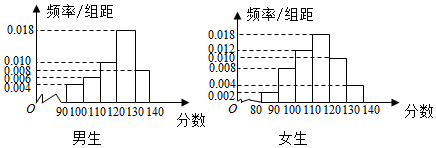 某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | 13 | 10 | 23 |
| 女生 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com