
分析 (1)不等式两边同时加$\sqrt{a}+\sqrt{b}$,在左边分组使用基本不等式即可得出结论;
(2)利用基本不等式得出ab的范围,将$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$通分得出结论.
解答 证明:(1)∵$\frac{a}{\sqrt{b}}+\sqrt{b}$≥2$\sqrt{a}$,$\frac{b}{\sqrt{a}}+\sqrt{a}$≥2$\sqrt{b}$,
∴$\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}$+$\sqrt{a}$+$\sqrt{b}$≥2$\sqrt{a}$+2$\sqrt{b}$,
∴$\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}$≥$\sqrt{a}+\sqrt{b}$.
(2)∵$\sqrt{ab}$≤$\frac{a+b}{2}$=$\frac{1}{2}$,
∴$\frac{1}{ab}$≥4,
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$=$\frac{a+b}{ab}+\frac{1}{ab}$=$\frac{2}{ab}$≥8.
点评 本题考查了基本不等式的变型与应用,不等式的证明,属于中档题.


科目:高中数学 来源: 题型:解答题
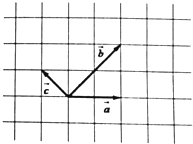 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
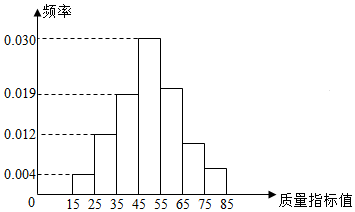 从某次知识竞赛中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85)内的频率之比为4:2:1.
从某次知识竞赛中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85)内的频率之比为4:2:1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com