
【题目】已知椭圆C: ![]() (a>b>0)的两个焦点F1 , F2和上下两个顶点B1 , B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
(a>b>0)的两个焦点F1 , F2和上下两个顶点B1 , B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
(1)求椭圆C的方程;
(2)过右焦点F2 , 斜率为k(k≠0)的直线与椭圆C相交于E,F两点,A为椭圆的右顶点,直线AE,AF分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.求证:kk′为定值.
【答案】
(1)解:由题意可得a=2, ![]() ,c=1.
,c=1.
∴椭圆C的方程为 ![]()
(2)解:设过点F2(1,0)的直线l的方程为:y=k(x﹣1).
设点E(x1,y1),F(x2,y2),联立 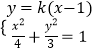 ,化为(3+4k2)x2﹣8k2x+4k2﹣12=0.
,化为(3+4k2)x2﹣8k2x+4k2﹣12=0.
显然△>0,∴ ![]() ,
, ![]() (*).
(*).
直线AE的方程为 ![]() ,直线AF的方程为
,直线AF的方程为 ![]() ,
,
令x=3,得点M ![]() ,N
,N ![]() .
.
∴点P ![]() .
.
直线PF2的斜率为k′= 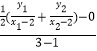
= ![]()
= ![]()
= ![]() .
.
把(*)代入得k′= ![]()
 =﹣
=﹣ ![]() .
.
∴ ![]() 为定值
为定值
【解析】解:(1)由题意利用菱形和含30°角的直角三角形的性质可得a=2, ![]() ,c=1.即可得到椭圆C的方程.(2)设过点F2(1,0)的直线l的方程为:y=k(x﹣1).设点E(x1 , y1),F(x2 , y2),与椭圆方程联立即可得到根与系数的关系,.可得直线AE的方程及直线AF的方程,令x=3,得点M,N的坐标.利用中点坐标公式可得点P的坐标.即可得到直线PF2的斜率为k′,把根与系数代入即可得出kk′为定值.
,c=1.即可得到椭圆C的方程.(2)设过点F2(1,0)的直线l的方程为:y=k(x﹣1).设点E(x1 , y1),F(x2 , y2),与椭圆方程联立即可得到根与系数的关系,.可得直线AE的方程及直线AF的方程,令x=3,得点M,N的坐标.利用中点坐标公式可得点P的坐标.即可得到直线PF2的斜率为k′,把根与系数代入即可得出kk′为定值.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+x﹣1)ex , 其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=﹣1,函数f(x)的图象与函数g(x)=![]() x3+
x3+![]() x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1) 求圆![]() 的方程;
的方程;
(2)问是否存在满足以下两个条件的直线![]() :①斜率为
:①斜率为![]() ;②直线被圆
;②直线被圆![]() 截得的弦为
截得的弦为![]() ,以
,以![]() 为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是错误命题的个数有( )
(1)若命题p为假命题,命题![]() 为假命题,则命题“
为假命题,则命题“![]() ”为假命题;
”为假命题;
(2)命题“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”;
”;
(3)对立事件一定是互斥事件;
(4)![]() 为两个事件,则P(A∪B)=P(A)+P(B);
为两个事件,则P(A∪B)=P(A)+P(B);
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],若成绩大于等于90分的人数为36,则成绩在[110,130)的人数为( ) 
A.12
B.9
C.15
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com