
解析:a+ b=(2,-1,-2)+(0,-1,4)
=(2+0,-1+(-1),-2+4)
=(2,-2,2);
a-b=(2,-1,-2)-(0,-1,4)
=(2-0,-1+1,-2-4)=(2,0,-6);
a·b=(2,-1,-2)·(0,-1,4)
=2×0+(-1)×(-1)+(-2)×4=-7;
(2a)·(-b)=-2(a·b)=-2×(-7)=14;
(a+ b)·(a-b)=(2,-2,2)·(2,0,-6)=2×2-2×0+2×(-6)=-8.
温馨提示:计算(2a)·(-b),既可以利用运算律把它化成-2(a·b),也可以求出2a、-b后,再点乘.计算(a+ b)·(a-b),既可以求出a+ b、a-b后,再点乘,也可以把(a+ b)·(a-b)写成a2-b2后计算.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:2012年人教A版高中数学必修四2.3平面向量基本定理及坐标表示(二)(解析版) 题型:填空题
在坐标平面内,已知A(2,1),B(0,2),C(-2,1),O(0,0),给出下面的结论:
①直线OC与直线BA平行;
②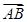 +
+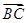 =
=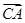 ;
;
③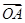 +
+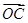 =
=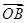 ;
;
④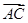 =
=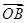 -2
-2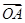 .
.
其中所有正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com